维基百科

菊池線 (物理)

菊池线（日语：菊池線／きくちせん，英語：Kikuchi lines）是电子散射形成的图形。它们结合在一起形成单晶样品的电子衍射带，在那里作为“定向空间的道路”，对于不确定他们所看到的是什么。在透射电子显微镜中，它们很容易在样品厚度足以进行多次散射的区域的衍射中被看到。[1]当晶体倾斜时，衍射点会忽亮忽暗，与此不同，菊池带用明确定义的交叉点(称为区域或极点)以及连接一个交叉点到下一个交叉点的路径来标记方向空间。

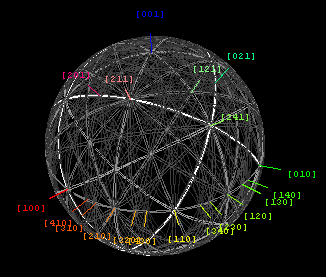
六边形蓝宝石(Al2O3)中300 keV电子的菊池线对下降到1/1Å的示意图，并标记了一些交叉点

菊池带几何的实验和理论图，以及它们的直接空间类似物，如弯曲轮廓、电子沟道模式和条纹可见性图，在晶体和纳米晶材料的电子显微镜学中越来越有用。[2]因为每条菊池线都与一组晶格平面的一侧的布拉格衍射有关，所以这些线可以用相同的密勒指数或倒数晶格指数来标记，这些指数用来识别单个的衍射点。另一方面，菊池带交点或区域用直接格指数来进行表示，即表示格基向量a、b和c的整数倍的表示方法。

菊池线是由散射的电子形成的衍射图案，例如由于热原子振动的结果。[3]它们的主要几何特征可以从菊池正士在1928年提出的一个简单的弹性机制中推断出来，[4]尽管需要用漫射非弹性散射的动力学理论来定量地理解它们。[5]

在X射线散射中，这些线被称为科塞尔线[6](以瓦尔特·科塞尔的名字命名)。

记录实验中的菊池图案和示意图 编辑

 
用300kev电子束拍摄的单晶硅聚敛光束衍射图中的菊池线

左边的图显示了通向硅[100]区的菊池线，其光束方向离(004)菊池带的区域约7.9度。在图像的动态范围是如此之大，只有部分胶片没有过度曝光。对于适应黑暗环境的眼睛来说，在荧光屏上捕捉菊池线要比在纸上或胶片上捕捉静止状态要容易得多，尽管眼睛和摄影介质对光照强度都有大致对数的响应。因此，电荷耦合器件的大线性动态范围有助于对这些衍射特征进行充分的定量研究。[7]

这幅图像对应的角度范围超过10度，需要使用比通常的相机长度L更短的相机。菊池的带宽本身(大约是倍角/d，其中倍角/d大约是对应平面布拉格角的两倍)远低于1度，因为电子的波长倍(在这种情况下大约是1.97皮)远小于格点平面的d-间距本身。相比之下，硅(022)的d-间距约为192皮，而硅(004)的d-间距约为136皮。

该图像取自晶体的一个区域，该区域比非弹性平均自由路径(大约200纳米)厚，因此漫射散射特征(菊池线)与相干散射特征(衍射点)相比会更强。幸存的衍射点出现在由明亮的菊池线相交的圆盘上，这一事实意味着衍射图案是用会聚的电子束拍摄的。在实践中，菊池线在选定区域或会聚束电子衍射图案的厚区域很容易看到，但是在小于100纳米的晶体的衍射中很难看到(在那里晶格条纹的可见性效应变得很重要)。这个图像是用会聚光束记录的，因为会聚光束缩小了必须记录在胶片上的对比度范围。

编译覆盖范围超过1个球面度的菊池图像需要拍摄许多倾斜变化的图像(例如在每个方向上变化2度)。这可能是一项乏味的工作，但在研究结构未知的晶体时可能有用，因为它可以清楚地揭示三维晶格的对称性。[8]

菊池线示意图及其立体投影 编辑

 
[001]区域钻石面心立方晶体的菊池线示意图
 
fcc晶体中8个<111>区域中的4个区域的倾斜度变化

左边的图为硅的方向空间的更大的部分绘制了菊池线。底部的大[011]区和[001]区之间的夹角为45度。请注意，右下角的四重区(此处标记为[001])与上面实验模式中标记为[100]的区域具有相同的对称性和方向，尽管该实验模式仅对10度左右。

还要注意的是，左边的图形是从以那个[001]区域为中心的立体投影中摘录的。这种保角投影允许我们将球面映射到一个平面上，同时保持局部的交角，从而保持区域的对称性。绘制这样的图需要一个人能够画出具有非常大曲率半径的圆弧。例如，左边的图形是在计算机出现之前画的，因此需要使用长臂圆规。如今，找到一个长臂圆规可能相当困难，因为在计算机的帮助下，绘制具有较大曲率半径(二维或三维)的曲线要容易得多。

立体图的保角效果在右图中更为明显，它对面心晶体或立方致密晶体(如金或铝)的取向空间进行了整整180度的倾斜。动画遵循<111>区域之间的面心立方晶体的{220}流苏可见带，在该点旋转60度设置旅行通过重复原始序列到下一个<111>区域。边缘-可见带与菊池带具有相同的全局几何结构，但是对于较薄的样本，它们的宽度与d间距成比例(而不是反比)。虽然用菊池带实验获得的角场宽度(和倾斜范围)通常要小得多，但动画提供了一个广角视图，说明菊池带如何帮助有见识的晶体学家在单个晶体标本的方向空间中找到标示。

真实空间类似物 编辑

 
一个硅[100]弯曲轮廓，好似一个蜘蛛被困在一个大约500纳米宽的椭圆形区域上

在较厚的样品的衍射图像中，菊池线用来突出晶格面上的边缘。由于高能电子衍射中的布拉格角非常小(300 keV时约为1⁄4度)，菊池带在倒数空间中相当狭窄。这也意味着在真实空间图像中，晶格平面的边缘不是由漫射散射特征装饰的，而是与相干散射相关联的。这些相干散射特性包括添加衍射(负责弯曲轮廓曲线箔),更多的电子渗透(产生电子在晶体表面的扫描电子图像引导模式),和晶格条纹反差(结果依赖的晶格条纹强度梁取向与试样厚度)。虽然细节对比不同，但这些特征的格平面轨迹几何与菊池图是相同的。

弯曲轮廓和摇摆曲线 编辑

 
弯曲轮廓和晶格条纹可见度是试样厚度和梁倾斜的函数

摇摆曲线(左)[9]是散射电子强度的图，它是入射电子束与样品中一组晶格平面法线夹角的函数。当这个角度从侧面(在这个方向上，电子束平行于晶格平面并垂直于它们的法线)向任何方向改变时，光束进入布拉格衍射状态，更多的电子在显微镜的后焦平面孔径外被衍射，产生如图中所示的弯曲硅箔所示的黑线对带。

[100]这幅图的弯曲轮廓“蜘蛛”被困在一个硅的区域中，硅的形状像一个椭圆形的手表玻璃，尺寸小于一微米，用300 keV电子成像。如果你倾斜水晶，蜘蛛移动到椭圆形的边缘，好像它试图出去。例如，在这幅图像中，当样本向左倾斜时，蜘蛛的[100]交叉点移到了椭圆的右边。

“蜘蛛”的腿和它们的交叉点可以被索引，就像上面关于实验性菊池图案的章节中接近[100]的菊池图案一样。原则上，我们可以使用这个弯曲轮廓来模拟箔片在椭圆上所有点上的矢量倾斜(毫弧度精度)。

格状条纹可见度图 编辑

从上面的摇摆曲线可以看出,随着试样厚度为10纳米和小范围(例如300 keV附近电子和晶格间距0.23海里)倾斜的角度范围,产生衍射和/或晶格条纹对比试样厚度成反比。因此，晶格条纹的几何形状在纳米材料的电子显微镜研究中非常有用，[10][11]正如弯曲轮廓线和菊池线在研究单晶样品(例如厚度在10微米范围内的金属和半导体样品)中很有用一样。例如，纳米结构的应用包括:(i)从不同倾斜度下拍摄的图像中确定单个纳米颗粒的三维晶格参数，[12](ii)随机取向的纳米颗粒采集的条纹指纹，(iii)基于倾斜度下条纹对比度变化的颗粒厚度图，(iv)从随机取向的纳米颗粒晶格图像中检测二十面体孪晶，(v)分析纳米颗粒与圆柱支架的取向关系。

电子沟道图 编辑

 
用300keV电子构造布里渊区

上述技术都涉及检测电子通过一个薄标本，通常在透射电子显微镜。另一方面，扫描电子显微镜，当一个聚焦的电子束光栅穿过一个厚的标本时，典型的观察电子“被激活”。电子沟道模式是在扫描电子显微镜次级和/或背散射电子图像中显示的与边缘晶格平面相关的对比效应。

对比效应与弯曲等高线相似，即在衍射条件下进入晶体表面的电子倾向于通过通道(在不损失能量的情况下更深入地穿透试件)，从而在靠近进入表面处激发更少的电子进行探测。因此，条带的形成取决于光束/晶格的方向，与现在熟悉的菊池线几何。

第一张扫描电子显微镜(SEM)图像是硅钢的电子沟道造影。[13]然而，这种技术的实际应用是有限的，因为通常只有一层薄薄的磨损损伤或非晶涂层就足以模糊对比度。[14]如果标本在检查前必须涂上一层导电涂层以防止充电，这也会模糊对比。在切割表面和原子尺度上自组装的表面上，电子沟道模式很可能在未来几年在现代显微镜上得到越来越多的应用。

另见 编辑

参考文献 编辑

  1. ^ David B. Williams; C. Barry Carter. Transmission electron microscopy: A textbook for materials science . Plenum Press, NY. 1996. ISBN 978-0-306-45324-3. 
  2. ^ K. Saruwatari; J. Akai; Y. Fukumori; N. Ozaki; H. Nagasawa; T. Kogure. Crystal orientation analyses of biominerals using Kikuchi patterns in TEM. J. Mineral. Petrol. Sci. 2008, 103: 16–22. 
  3. ^ Earl J. Kirkland. Advanced computing in electron microscopy. Plenum Press, NY. 1998: 151. ISBN 978-0-306-45936-8. 
  4. ^ S. Kikuchi. Diffraction of Cathode Rays by Mica. Japanese Journal of Physics. 1928, 5 (3061): 83–96. Bibcode:1928Natur.121.1019N. doi:10.1038/1211019a0. 
  5. ^ P. Hirsch; A. Howie; R. Nicholson; D. W. Pashley; M. J. Whelan. Electron microscopy of thin crystals. Butterworths/Krieger, London/Malabar FL. 1977. ISBN 978-0-88275-376-8. 
  6. ^ R. W. James. Chapter VIII. The Optical Principles of the Diffraction of X-Rays'. Ox Bow Press, Woodbridge, Connecticut. 1982. ISBN 978-0-918024-23-7. 
  7. ^ J. C. H. Spence and J. Zuo. Ch. 9. Electron microdiffraction. Plenum, New York. 1992. ISBN 978-0-306-44262-9. 
  8. ^ E. Levine; W. L. Bell; G. Thomas. Further applications of Kikuchi diffraction patterns; Kikuchi maps. Journal of Applied Physics. 1966, 37 (5): 2141–2148. Bibcode:1966JAP....37.2141L. doi:10.1063/1.1708749. 
  9. ^ H. Hashimoto; A. Howie; M. J. Whelan. Anomalous Electron Absorption Effects in Metal Foils: Theory and Comparison with Experiment. Proceedings of the Royal Society A. 1962, 269 (1336): 80. Bibcode:1962RSPSA.269...80H. doi:10.1098/rspa.1962.0164. 
  10. ^ P. Fraundorf; Wentao Qin; P. Moeck; Eric Mandell. Making sense of nanocrystal lattice fringes. Journal of Applied Physics. 2005, 98 (11): 114308–114308–10. Bibcode:2005JAP....98k4308F. arXiv:cond-mat/0212281  . doi:10.1063/1.2135414. 
  11. ^ P. Wang; A. L. Bleloch; U. Falke; P. J. Goodhew. Geometric aspects of lattice contrast visibility in nanocrystalline materials using HAADF STEM. Ultramicroscopy. 2006, 106 (4–5): 277–283. doi:10.1016/j.ultramic.2005.09.005. 
  12. ^ Wentao Qin; P. Fraundorf. Lattice parameters from direct-space images at two tilts. Ultramicroscopy. 2003, 94 (3–4): 245–262. PMID 12524195. arXiv:cond-mat/0001139  . doi:10.1016/S0304-3991(02)00335-2. 
  13. ^ Knoll M. Aufladepotentiel und sekundäremission elektronenbestrahlter körper (Static potential and secondary emission of bodies under electron irradiation). Z. Tech. Phys. 1935, 11: 467–475. 
  14. ^ J. I. Goldstein; D. E. Newbury; P. Echlin; D. C. Joy; A. D. Romig Jr.; C. E. Lyman; C. Fiori; E. Lifshin. Scanning electron microscopy and X-ray microanalysis. Plenum Press, NY. 1992. ISBN 978-0-306-44175-2. 
取自“https://zh.wikipedia.org/w/index.php?title=菊池線_(物理)&oldid=77748985”