约翰逊多面体
Johnson多面體,又譯詹森多面体或莊遜多面體,是指每個面都是正多邊形的嚴格凸多面體(凸正多邊形多面體)。其不要求每個面皆要是相同的多邊形,也不要求每個頂角要相等。詹森多面體的一個例子是正四角錐(J1),其由4個正三角形和1個正方形組成。一些作者會將詹森多面體定義為正多面體、半正多面體、均勻多面體、棱柱、反棱柱之外,所有由正多邊形面組成的凸多面體。這些立體由諾曼·詹森在1966年命名;1969年,維克托·查加勒證明只有92個這樣的立體。
| 部分的詹森多面體 | |
|---|---|
 正五角罩帳 (罩帳) |
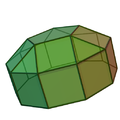 正五角帳塔柱 (組合立體) |
 正二十面體欠鄰二側錐 (切割立體) |
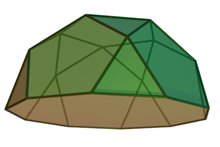
 球狀屋頂 (基本立體) |



在任何嚴格凸多面體中,每個頂點至少要是三個面的公共頂點,而且這些面的角度總和要小於360度。由於正多邊形的角度至少為60度,因此每個頂點最多只能是5個面的公共頂點。正五角錐(J2)就是一個包含了有五個面的公共頂點之頂點的一個例子。
雖然沒有明確限制組成詹森多面體之多邊形面的邊數,但事實證明,所有非正多面體、半正多面體、均勻多面體、棱柱、反棱柱的詹森多面體的面都是由三、 四、 五、 六、 八或十邊形組成。
1966年,諾曼·詹森給出了一個詹森多面體的清單,裡面包含了92種詹森多面體(不包括5個柏拉圖立體、13個阿基米德立體、無限多的柱狀均勻多面體,即棱柱和反棱柱)並給予了名稱和編號。[1]他並沒有證明這些立體僅有92個,但他確實猜想不存在其他這種性質的立體。維克托·查加勒在1969年証明諾曼·詹森所列出的92種詹森多面體是完整的,不存在其他有此性質的立體。
在詹森多面體中異相雙四角帳塔柱又稱為偽小斜方截半立方体[2],是唯一一個具有局部等角的特性,其所有頂點都是3個正方形和1個三角形的公共頂點。然而其不完全具備點可遞的特性,也就是存在有一組頂點無法透過將立體旋轉、平移或鏡射等幾何變換將頂點變換到另外一個頂點,或者說其頂點並沒有全部位於同一個對稱性的軌道內,因此其只能算是詹森多面體無法歸類在阿基米德立體。[4]
命名 编辑
詹森多面體的命名遵循著一個靈活且精確的描述規則。因此許多詹森多面體可以用不同的方式命名,而不會影響其描述的準確性。大多數詹森多面體可以由前幾種棱錐、帳塔、罩帳、柏拉圖立體、阿基米德立體、棱柱和反棱柱構成;特定立體的名稱的反映這些成分。其命名主要從這些立體開始,加入一系列前綴或後綴到單詞上以表示添加、切割和旋轉等變換:
- 「雙-」(Bi-[<>])兩個相同的立體底面對底面貼合所形成的立體。對於帳塔和罩帳,組合的結果還可以分成相同相位(「同相-」,ortho-)和不同相位(「異相-」,gyro-[*])兩種。正八面體在此命名規則下可以命名為雙四角錐[4<>]。
- 「-柱」(Elongated[=])代表在目標立體的其中一個底面疊上角柱。若同時包含「雙-」前綴,則代表角柱包夾在雙立體的兩立體之間。小斜方截半立方体在此命名規則下可以命名為同相雙四角帳塔。
- 「-反角柱」或「-反棱柱」(Gyroelongated[z])代表在目標立體的其中一個底面疊上反角柱。若同時包含「雙-」前綴,則代表反角柱包夾在雙立體的兩立體之間。正二十面體在此命名規則下可以命名為雙五角錐反角柱[5<z>]。
- 「側立體-」(Augmented[+])表示在立體的側面上疊上特定立體,例如「側錐-」表示在目標立體的側面上疊上錐體、「側台塔-」表示在目標立體的側面上疊上台塔、「側丸塔-」表示在目標立體的側面上疊上丸塔。
- 「-欠立體」(Diminished[-])表示目標立體缺少局部的結構,例如正二十面體欠側錐表示少從正二十面體上切去一個側錐(五角錐)的結果。
- 「旋-」(Gyrate[*])表示旋轉立體上的局部特定結構。
後三種操作「側立體-」、「-欠立體」和「旋-」可在同個較大的立體上重複套用,因此還有「二-」(Bi-)、「三-」(Tri-)的前綴,表示該種操作的套用次數,例如「二側錐-」表示在目標立體的兩個面上疊上錐體、「二旋側帳塔-」代表該立體有兩個側帳塔的局部構造被旋轉、「-欠三側錐」代表從目標立體切去三個側錐的結果。
在面數較多的立體中,「側立體-」和「-欠立體」操作可以作用於相對面和非相對面。對於相對面,會用前綴「對-」(Para-)來稱之,而非相對面的情況在詹森多面體可能是相鄰的,因此會用前綴「鄰-」(meta-)稱之,另一種情況則是有相隔一個面,此時則以「間-」稱之。
最後幾個詹森多面體的名稱是基於其構成的多邊形組合來命名的。其名稱由諾曼·詹森使用以下命名法命名[5]:
- “新月”(lune)定義為在正方形兩對側各有一個三角形的多邊形組合,也就是三角形-正方形-三角形帶。[6]
- “屋頂”(Spheno-,日語:屋根)表示由兩個相鄰“新月”組成的楔形多邊形組合。
- “廣底...屋頂”(Hebespheno-,日語:広底...屋根)表示有三個“新月”狀組成,其中第三個“新月”狀插在兩個“新月”狀中間,形成的鈍狀多邊形組合。
- “球狀-”(Corona,日語:球形-)表示由八個三角形組成的冠狀多邊形組合。
- “加長型球狀-”(Megacorona,日語:長球形-)表示由12個三角形組成,比“球狀”更大的冠狀多邊形組合。
分類 编辑
Johnson多面體的構成方法之一是將其他由正多邊形面組成的凸多面體和下面幾種立體的拼合:
- 棱錐:以正三、四、五邊形為底而成的角錐。如:正四角錐(J1)、正五角錐(J2)
- 帳塔(平頂塔):有兩個在空間中平行的正多邊形,其中一個的邊數是另一個的兩倍。在兩者間加入三角形和正方形。如:正三角帳塔(J3)、正四角帳塔(J4)、正五角台塔(J5)。
- 罩帳:有兩個在空間中平行的正多邊形,其中一個的邊數是另一個的兩倍。在兩者間加入三角形和正五邊形。如:正五角罩帳(J6)、正五角罩帳反角柱(J25)。
另一種方法就是將這些凸多面體「切除」或「加上」一些立體。如:小斜方截半二十面體欠一側台塔(J76)。也有一些是將這些凸多面體旋轉局部來構成。如:單旋側帳塔小斜方截半二十面體(J72)。[7]
立體介紹 编辑
棱錐及塔 编辑
前6個詹森多面體是底面邊數少於5的棱錐、台塔或丸塔。底面邊數達到6或以上若要讓面維持正多邊形的話要嘛共面要嘛無法構造僅能以非正多邊形存在因此不屬於詹森多面體。[9]:115
錐體 编辑
前2個詹森多面體J1及J2是錐體,分別為正四角錐和正五角錐。正三角錐因為是正多面體(正四面體)所以不算在詹森多面體內。這些立體皆代表正多面體的局部。
| 正多面體 3> T |
J1 4> |
J2 5> |
|---|---|---|
| 正三角錐 (正四面體) |
正四角錐 | 正五角錐 |
| 相關正多面體 | ||
| 正四面體 | 正八面體 | 正二十面體 |
台塔 编辑
接下來3個詹森多面體J3、J4、J5是台塔,分別是正三角台塔、正四角台塔和正五角台塔。正二角台塔已退化為三角柱,而三角柱算是均勻多面體,因此也不算在詹森多面體內。
| 台塔 | ||||
|---|---|---|---|---|
| 均勻多面體 | J3 3c aC- |
J4 4c |
J5 5c | |
| 正二角台塔 (三角柱) |
正三角台塔 | 正四角台塔 | 正五角台塔 | |
| 相關均勻多面體 | ||||
| 截半立方體 | 小斜方截半立方体 | 小斜方截半二十面体 | ||
丸塔 编辑
接下來的1個詹森多面體J6是丸塔,即正五角丸塔。正四角丸塔和正六角丸塔因無法滿足所有面皆為正多邊形的條件,因此不屬於詹森多面體。
| 丸塔 | ||||
|---|---|---|---|---|
| 非詹森多面體 4r |
J6 5r aD- |
非詹森多面體 6r | ||
| 正四角丸塔 | 正五角丸塔 | 正六角丸塔 | ||
| 相關均勻多面體 | ||||
| 截半二十面体 | ||||
錐體衍生 编辑
詹森多面體編號7至11是由錐體衍生而來。
錐柱及錐反角柱 编辑
錐柱及錐反角柱皆為錐體與各種柱狀立體組合而成,其中,錐柱為錐體和柱體底面對體面疊合而成;而錐反角柱為錐體和反角柱底面對體面疊合而成。
錐柱及錐反角柱被歸類為詹森多面體的最大底面邊數皆僅有5,也就是六角錐柱和六角錐反角柱皆不屬於詹森多面體。特別地,在錐反角柱,底面邊數為3的三角錐反角柱也不是詹森多面體,因為三角反角柱若要滿足所有面都是正多邊形的條件時,會產生互相共面的面。
| 錐柱 | 錐反角柱 | ||||
|---|---|---|---|---|---|
| J7 3=> |
J8 4=> |
J9 5=> |
共面 | J10 4z> |
J11 5z> I- |
| 正三角錐柱 | 正四角錐柱 | 正五角錐柱 | 正三角錐反角柱 (三方半偏方面體) |
正四角錐反角柱 | 正五角錐反角柱 |
| 組合的多面體 | |||||
| 正三角錐 三角柱 |
正四角錐 立方體 |
正五角錐 五角柱 |
正三角錐 正三角反棱柱 |
正四角錐 正四角反棱柱 |
正五角錐 正五角反棱柱 |
雙錐、雙錐柱及雙反角錐柱 编辑
在雙錐體中,歸類為詹森多面體底面邊數最大為5,即雙五角錐,而雙四角錐若滿足所有面都是正多邊形的條件會變成正多面體(正八面體)因此沒有歸類在詹森多面體中。而雙錐柱在底面邊數為3、4和5時皆為詹森多面體。雙反角錐柱則是在底面邊數為5時,也就是雙五角錐反角柱若滿足所有面都是正多邊形的條件會變成正多面體(正二十面體)因此沒有歸類在詹森多面體中;而底面邊數為3時若滿足所有面都是正多邊形的條件時,其面會出現共面的情況,因此也不屬於詹森多面體。
| 雙錐體 | 雙錐柱 | 雙反角錐柱 | ||||||
|---|---|---|---|---|---|---|---|---|
| J12 3<> |
正多面體 4<> |
J13 5<> |
J14 3<=> |
J15 4<=> |
J16 5<=> |
共面 3<z> |
J17 4<z> |
正多面體 5<z> |
| 雙三角錐 | 雙四角錐 (正八面體) |
雙五角錐 | 雙三角錐柱 | 雙四角錐柱 | 雙五角錐柱 | 雙三角錐反角柱 (三方偏方面體) |
雙四角錐反角柱 | 雙五角錐反角柱 (正二十面體) |
| 組合的多面體 | ||||||||
| 正三角錐 | 正四角錐 | 正五角錐 | 正三角錐 三角柱 |
正四角錐 立方體 |
正五角錐 正五角柱 |
正三角錐 正三角反棱柱 |
正四角錐 正四角反棱柱 |
正五角錐 正五角反棱柱 |
帳塔及罩帳衍生 编辑
詹森多面體編號18至48是由帳塔及罩帳衍生而來。
帳塔及丸塔與柱體或反柱體組合 编辑
帳塔及丸塔與柱體或反柱體可以組合出帳塔柱(帳塔與稜柱的組合)、丸塔柱(丸塔與稜柱的組合)、台塔反角柱(台塔與反角柱的組合)和丸塔反角柱(丸塔與反角柱的組合)。
這些立體被歸類為詹森多面體的最高底面邊數同樣是5,即正五角台塔柱、正五角罩帳柱、正五角台塔反角柱和正五角罩帳反角柱。同樣在丸塔的組合中,僅有底面邊數為5的正五角罩帳柱和正五角罩帳反角柱是詹森多面體,底面邊數是4或以下、6或以上皆無法滿足所有面都是正多邊形的情況。而所有這些立體在底面邊數為2的情況也非詹森多面體,其中,正二角台塔柱會出現共面的情況,而正二角台塔反角柱則為凹多面體。
| 帳塔柱 | 丸塔柱 | 台塔反角柱 | 丸塔反角柱 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 共面 | J18 3c= |
J19 4c= eC- |
J20 5c= |
J21 5r= |
凹多面體 | J22 3cz |
J23 4cz |
J24 5cz |
J25 5rz |
| 正二角台塔柱 | 正三角台塔柱 | 正四角台塔柱 | 正五角台塔柱 | 正五角罩帳柱 | 正二角台塔反角柱 | 正三角台塔反角柱 | 正四角台塔反角柱 | 正五角台塔反角柱 | 正五角罩帳反角柱 |
| 組合的多面體 | |||||||||
| 四角柱 三角柱 |
六角柱 正三角台塔 |
八角柱 正四角台塔 |
十角柱 正五角台塔 |
十角柱 正五角罩帳 |
四角反棱柱 三角柱 |
六角反棱柱 正三角台塔 |
八角反棱柱 正四角台塔 |
十角反棱柱 正五角台塔 |
十角反棱柱 正五角罩帳 |
雙台塔 编辑
雙台塔為兩個台塔底面對底面貼合所形成的立體。在凸多面體的情況下,又可以分成同相雙台塔和異相雙台塔。其是否屬於詹森多面體與台塔的情況類似,然而也有一些例外情況,例如異相雙三角台塔在所有面都是正多邊形的條件下會是一種阿基米德立體——截半立方體,所以不會被歸類在詹森多面體中。[10]
| 同相雙台塔 | 異相雙台塔 | ||||||
|---|---|---|---|---|---|---|---|
| 共面 | J27 3cc |
J28 4cc |
J30 5cc |
J26 2cc* |
半正多面體 | J29 4cc* |
J31 5cc* |
| 同相雙楔體 | 同相雙三角台塔 | 同相雙四角台塔 | 同相雙五角台塔 | 異相雙三角柱 | 異相雙三角台塔 (截半立方體) |
異相雙四角柱 | 異相雙五角柱 |
| 組合的多面體 | |||||||
| 三角柱 | 三角台塔 | 四角台塔 | 五角台塔 | 三角柱 | 三角台塔 | 四角台塔 | 五角台塔 |
台塔丸塔與雙丸塔 编辑
台塔丸塔為台塔與丸塔的組合,而雙丸塔則為兩個丸塔底面對底面貼合所形成的立體,兩者在凸多面體的條件下與雙台塔一樣可分為同相與異相,分別為同相台塔丸塔、異相台塔丸塔、同相雙丸塔和異相雙丸塔。與丸塔的情況一樣,僅有底面邊數為5的情況時能被歸類在詹森多面體,即同相五角台塔丸塔、異相五角台塔丸塔、同相雙五角罩帳和異相雙五角丸塔。而異相雙五角丸塔若在所有面都是正多邊形的條件下,則其與截半二十面体無異[11]。
| 台塔丸塔 | 雙丸塔 | ||
|---|---|---|---|
| J32 5cr |
J33 5cr* |
J34 5rr aD* |
半正多面體 |
| 同相五角台塔丸塔 | 異相五角台塔丸塔 | 同相雙五角丸塔 | 異相雙五角丸塔 (截半二十面体) |
| 組合的多面體 | |||
| 五角台塔 五角丸塔 |
五角丸塔 | ||
雙台塔柱 编辑
雙台塔柱為在雙台塔的兩個台塔中間再加一個柱體所構成的立體,與雙台塔一樣,可分成同相與異相。其中,同相雙四角台塔柱在所有面都是正多邊形的條件下與小斜方截半立方体等價。
| 同相雙台塔柱 | 異相雙台塔柱 | ||||||
|---|---|---|---|---|---|---|---|
| 共面 | J35 3c=c |
半正多面體 | J38 5c=c |
共面 | J36 3c=c* |
J37 4c=c* eC* |
J39 5c=c* |
| 同相雙二角台塔柱 | 同相雙三角台塔柱 | 同相雙四角台塔柱 (小斜方截半立方体) |
同相雙五角台塔柱 | 異相雙二角台塔柱 | 異相雙三角台塔柱 | 異相雙四角台塔柱 | 異相雙五角台塔柱 |
| 組合的多面體 | |||||||
| 四角柱 三角柱 |
六角柱 三角台塔 |
八角柱 四角台塔 |
十角柱 五角台塔 |
四角柱 三角柱 |
六角柱 三角台塔 |
八角柱 四角台塔 |
十角柱 五角台塔 |
台塔丸塔柱與雙丸塔柱 编辑
台塔丸塔柱為在台塔丸塔兩底面相聯的中間再加入一個柱體構成的立體,而雙丸塔柱為在雙丸塔的兩個丸塔中間再加一個柱體所構成的立體。與帳塔罩帳與雙罩帳一樣,可分成同相與異相。這兩種立體和丸塔一樣,僅有底面邊數為5的情況可被歸類為詹森多面體。
| 台塔丸塔柱 | 雙丸塔柱 | ||
|---|---|---|---|
| J40 5c=r |
J41 5c=r* |
J42 5r=r |
J43 5r=r* |
| 同相五角台塔丸塔柱 | 異相五角台塔丸塔柱 | 同相五角雙丸塔柱 | 異相五角雙丸塔柱 |
| 組合的多面體 | |||
| 十角柱 五角台塔 五角丸塔 |
十角柱 五角丸塔 | ||
雙台塔反角柱、台塔丸塔反角柱與雙丸塔反角柱 编辑
雙台塔反角柱、台塔丸塔反角柱與雙丸塔反角柱皆為在原組合立體的底面與底面之間加入反角柱所組成的立體。與雙台塔柱、台塔丸塔柱與雙丸塔柱不同,雙台塔反角柱、台塔丸塔反角柱與雙丸塔反角柱並不分同相與異相,僅有在每個立體各存在手性鏡像。
| 雙台塔反角柱 | 台塔丸塔反角柱 | 雙丸塔反角柱 | |||
|---|---|---|---|---|---|
| 凹多面體 | J44 3czc |
J45 4czc |
J46 5czc |
J47 5czr |
J48 5rzr |
| 雙二角台塔反角柱 | 雙三角台塔反角柱 | 雙四角台塔反角柱 | 雙五角台塔反角柱 | 五角台塔丸塔反角柱 | 雙五角丸塔反角柱 |
| 組合的多面體 | |||||
| 三角柱 四角反棱柱 |
三角台塔 六角反棱柱 |
四角台塔 八角反棱柱 |
五角台塔 十角反棱柱 |
五角台塔 五角丸塔 十角反棱柱 |
五角丸塔 十角反棱柱 |
側錐柱體 编辑
詹森多面體編號49至57是側錐柱體。側錐柱體是指在柱體側面上疊上錐體所形成的立體。能在保持凸多面體和每個面都是正多邊形的情況下在側面加入錐體的柱體最大的底面邊數為6。三角柱三個側面都能加入錐體形成滿足詹森多面體條件的側錐三角柱,分別有側錐三角柱、二側錐三角柱和三側錐三角柱。[12]:86
四角柱不能在相鄰側面上疊上錐體,否則會變成凹多面體,因此四角柱最多只能加入兩個側錐,分別為側錐四角柱和二側錐四角柱,然而這兩個立體分別與四角錐柱和雙四角錐柱相同,因此不在此節列出。
五角柱也不能在相鄰側面上疊上錐體,否則會變成凹多面體,因此五角柱最多只能加入兩個側錐,分別為側錐五角柱和間二側錐五角柱。
六角柱同樣不能在相鄰側面上疊上錐體,否則會變成凹多面體,然而六角柱有六個側面,因此最多可以加入三個側錐。在加入兩個側錐的情況下,可以分成加在相對側面上的二側錐六角柱和加在相隔一個側面之側面上的二側錐六角柱,因此有對二側錐六角柱和間二側錐六角柱兩種。另外兩種屬於詹森多面體的側錐六角柱為側錐六角柱和三側錐六角柱。
| 側錐三角柱 | 側錐五角柱 | 側錐六角柱 | ||||||
|---|---|---|---|---|---|---|---|---|
| J49 3=+ |
J50 3=++ |
J51 3=+++ |
J52 5=+ |
J53 5=++ |
J54 6=+ |
J55 6=++ |
J56 6=+x |
J57 6=+++ |
| 側錐三角柱 | 二側錐三角柱 | 三側錐三角柱 | 側錐五角柱 | 間二側錐五角柱 | 側錐六角柱 | 對二側錐六角柱 | 間二側錐六角柱 | 三側錐六角柱 |
| 組合的多面體 | ||||||||
| 三角柱 四角錐 |
五角柱 四角錐 |
六角柱 四角錐 | ||||||
正多面體衍生 编辑
詹森多面體編號58至64的立體可以藉由在正多面體上疊上錐體或移除局部來構造。能夠形成詹森多面體的側錐正多面體有正四面體、立方體和正十二面體,而側錐正四面體同於雙三角錐因此不在此列出;側錐立方體與側錐四角柱、四角錐柱和雙四角錐柱相同因此也不在此列出,下表將列出側錐正十二面體的情況。
而能夠移除局部構成詹森多面體的正多面體有正二十面體。
側錐正十二面體 编辑
正十二面體不能在相鄰側面上疊上錐體,否則會變成凹多面體,因此正十二面體最多只能加入三個側錐。在加入兩個側錐的情況下,可以分成加在相對側面上的二側錐正十二面體和加在(相對)相鄰的側面上的二側錐正十二面體,因此有对二侧锥正十二面体和间二侧锥正十二面体兩種。
| J58 D+ |
J59 D++ |
J60 D+x |
J61 D+++ |
|---|---|---|---|
| 侧锥正十二面体 | 对二侧锥正十二面体 | 间二侧锥正十二面体 | 三侧锥正十二面体 |
| 組合的多面體 | |||
| 正十二面體和正五角錐 | |||
正二十面體欠側錐和側錐正二十面體欠側錐 编辑
可此從正二十面體移除五角錐來構造新的立體,稱為正二十面體欠側錐。最多可以從正二十面體移除3個五角錐。移除掉3個五角錐的正二十面體還可以進一步地在其中一個三角形面上疊上三角錐構成側錐正二十面體欠側錐。
| 正二十面體欠側錐 | 側錐正二十面體欠側錐 | |||
|---|---|---|---|---|
| J11 (重複) |
均勻多面體 | J62 I-/ |
J63 I--- |
J64 I---+ |
| 正二十面體欠一側錐 (五角錐反角柱) |
正二十面體欠對二側錐 (五角反棱柱) |
正二十面體欠鄰二側錐 | 正二十面體欠三側錐 | 側錐正二十面體欠三側錐 |
阿幾米德立體衍生 编辑
詹森多面體編號65至83的立體可以藉由在阿幾米德立體上疊上台塔、移除局部或旋轉局部來構造。
側台塔阿幾米德立體 编辑
能夠在面上疊上帳塔購造成詹森多面體的阿幾米德立體有截角四面體、截角立方體和截角十二面體。這些立體皆不能在相鄰面上疊上帳塔,否則會變成凹多面體。因此截角四面體僅有一個六邊形面可以疊上三角台塔;而截角立方體最多可以在兩個八邊形面上疊上四角台塔,對於疊上兩個四角台塔的情況,其必須疊在相對的八邊形面上。截角十二面體最多可以疊上3個五角台塔。
| 側台塔截角四面體 | 側台塔截角立方體 | 側台塔截角十二面體 | ||||
|---|---|---|---|---|---|---|
| J65 tT+ |
J66 tC+ |
J67 tC++ |
J68 tD+ |
J69 tD++ |
J70 tD+x |
J71 tD+++ |
| 側台塔截角四面體 | 側台塔截角立方體 | 對二側帳塔截角立方體 | 側台塔截角十二面體 | 對二側台塔截角十二面體 | 間二側台塔截角十二面體 | 三側台塔截角十二面體 |
| 組合的多面體 | ||||||
| 截角四面體 三角帳塔 |
截角立方體 四角帳塔 |
截角十二面體 五角帳塔 | ||||
旋轉局部或移除局部的阿幾米德立體 编辑
| 旋側帳塔小斜方截半二十面體 | |||
|---|---|---|---|
| J72 eD* |
J73 eD** |
J74 eD*' |
J75 eD*** |
| 單旋側帳塔小斜方截半二十面體 | 對二旋側台塔小斜方截半二十面體 | 鄰二旋側台塔小斜方截半二十面體 | 三旋側台塔小斜方截半二十面體 |
| 小斜方截半二十面體欠側帳塔 | |||
| J76 eD- |
J80 eD-- |
J81 eD-/ |
J83 eD--- |
| 小斜方截半二十面體欠一側台塔 | 小斜方截半二十面體欠對二側帳塔 | 小斜方截半二十面體欠鄰二側帳塔 | 小斜方截半二十面體欠三側台塔 |
| 旋側帳塔小斜方截半二十面體欠側帳塔 | |||
| J77 -* |
J78 -' |
J79 -** |
J82 --* |
| 對單旋側台塔小斜方截半二十面體欠一側台塔 | 鄰單旋側台塔小斜方截半二十面體欠一側台塔 | 二旋側台塔小斜方截半二十面體欠一側台塔 | 單旋側台塔小斜方截半二十面體欠二側台塔 |
此外還有一些其他立體也可以視為是旋轉局部或移除局部的阿幾米德立體,例如J37(異相雙四角帳塔柱)可以視為是旋轉一側四角台塔的小斜方截半立方體。
| J27 | J3 | J34 | J6 | J37 | J19 | 均勻多面體 |
|---|---|---|---|---|---|---|
| 單旋截半立方體 (同相雙三角台塔) |
截半立方體欠側帳塔 (三角帳塔) |
单旋截半二十面体 (同相雙五角丸塔) |
截半二十面體欠側帳塔 (五角罩帳) |
单旋小斜方截半立方体 (異相雙四角台塔柱) |
小斜方截半立方體欠側帳塔 (四角帳塔柱) |
小斜方截半立方體欠二側帳塔 (八角柱) |
| 旋轉局部或移除局部的多面體 | ||||||
| 截半立方體 | 截半二十面体 | 小斜方截半立方体 | ||||
基本立體 编辑
詹森多面體編號84至92的立體不能以切除、增加角錐、台塔、丸塔等方法取得。
扭稜反角柱 编辑
扭稜反角柱可以透過將反角柱截角後交錯來構造。可以構成詹森多面體的扭稜反角柱底面邊數最大只能到4,更大的底面邊數無法以所有面皆為正多邊形的形式存在;而扭稜三角反角柱若要滿足有面皆為正多邊形的條件則會與正二十面體無異,因此不列入詹森多面體。
| J84 | 正多面體 | J85 |
|---|---|---|
| 扭稜鍥形體 ss{2,4} |
正二十面體 ss{2,6} |
扭稜四角反角柱 ss{2,8} |
| 扭稜二角反角柱 | 扭稜三角反角柱 | 扭稜四角反角柱 |
其它立體 编辑
| J86 | J87 | J88 | |
|---|---|---|---|
| 球狀屋頂 (Sphenocorona) |
側錐球狀屋頂 (Augmented sphenocorona) |
加長型球狀屋頂 (Sphenomegacorona) | |
| J89 | J90 | J91 | J92 |
| 廣底加長型球狀屋頂 (Hebesphenomegacorona) |
五角錐球狀屋頂 (Disphenocingulum) |
雙新月雙罩帳 (Bilunabirotunda) |
三角廣底球狀罩帳 (Triangular hebesphenorotunda) |
外接球詹森多面體 编辑
有25個詹森多面體存在外接球,這意味著這25個詹森多面體的頂點都可以位於同一個球面上。這些立體包括編號為1至6、11、19、27、34、37、62、63和72至83的詹森多面體。這些立體皆與正多面體有分割、旋轉局部或移除局部的關聯。[13]
| 正八面體 | 截半立方體 | 小斜方截半立方体 | |||
|---|---|---|---|---|---|
| J1 |
J3 |
J27 |
J4 |
J19 |
J37 |
| 正二十面體 | 截半二十面体 | ||||
|---|---|---|---|---|---|
| J2 |
J11 |
J62 |
J63 |
J6 |
J34 |
| 小斜方截半二十面体 | ||||||
|---|---|---|---|---|---|---|
| J5 |
J72 |
J73 |
J74 |
J75 |
J76 |
J77 |
| J78 |
J79 |
J80 |
J81 |
J82 |
J83 | |
參考資料 编辑
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ GWH. Pseudo Rhombicuboctahedra. www.georgehart.com. [2018-04-17]. (原始内容存档于2012-12-08).
- ^ Grünbaum, Branko, An enduring error (PDF), Elemente der Mathematik, 2009, 64 (3): 89–101 [2022-12-31], MR 2520469, doi:10.4171/EM/120 , (原始内容存档 (PDF)于2014-05-07) Reprinted in Pitici, Mircea (编). The Best Writing on Mathematics 2010. Princeton University Press. 2011: 18–31..
- ^ Sommerville, D. M. Y., Semi-regular networks of the plane in absolute geometry, Transactions of the Royal Society of Edinburgh, 1905, 41: 725–747 [2022-12-31], doi:10.1017/s0080456800035560, (原始内容存档于2022-12-24). As cited by Grünbaum (2009)[3].
- ^ George Hart (quoting Johnson). Johnson Solids. Virtual Polyhedra. 1996 [2014-02-05]. (原始内容存档于2022-01-11).
- ^ The Bilunabirotunda. qfbox.info. [2022-09-09]. (原始内容存档于2022-09-09).
- ^ The Gyrate Rhombicosidodecahedron. www.qfbox.info. [2023-01-04]. (原始内容存档于2023-01-04).
- ^ George W. Hart. Johnson Solids. [2008-04-12]. (原始内容存档于2022-01-11).
- ^ MATHEMATICS IN ENGLISH (PDF). education.gov.za. [2023-01-01]. (原始内容存档 (PDF)于2023-01-10).
- ^ The Triangular Cupola. www.qfbox.info. [2022-12-31]. (原始内容存档于2023-01-03).
- ^ The Pentagonal Rotunda. www.qfbox.info. [2022-12-31]. (原始内容存档于2023-01-04).
- ^ Rajwade, A.R. Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. 2001. ISBN 9789386279064.
- ^ Klitzing, Dr. Richard. Johnson solids et al.. bendwavy.org. [2018-04-17]. (原始内容存档于2014-05-02).
- Victor A. Zalgaller. Convex Polyhedra with Regular Faces. Consultants Bureau. 1969. No ISBN. The first proof that there are only 92 Johnson solids.
外部連結 编辑
- Sylvain Gagnon之"Convex polyhedra with regular faces[永久失效連結]", Structural Topology, No. 6, 1982, 83-95.
- Paper Models of Polyhedra (页面存档备份,存于互联网档案馆)
- George W. Hart描述之Johnson多面體 (页面存档备份,存于互联网档案馆)
- 92種立體的圖片
- 埃里克·韦斯坦因. Johnson多面體. MathWorld.
- Johnson多面體虛擬模型
- Magnetic Blocks之Educational toy system for making Johnson solids and other polyhedra (页面存档备份,存于互联网档案馆)
- Vladimir Bulatov之Johnson多面體的虛擬模型 (页面存档备份,存于互联网档案馆)