動力系統

此條目頁的主題是數學概念。關於有關車輛中產生動力的來源，請見「動力總成」。

數學中，動力系統（dynamical system）是用函數描述環繞空間中某點隨時間的變化情況的系統，例如描述鐘擺晃動、管道中水的流動，或者湖中每年春季魚類的數量，凡此等等的數學模型都是動力系統。對時空測量的不同選擇中，最一般的定義統一了數學中的數個概念，如常微分方程和遍歷理論。時間可用整數、實數或複數甚至更一般的代數對象來度量；空間可以是流形，也可以是集合，無需在其上定義光滑的時空結構。

洛倫茨吸引子的動態系統

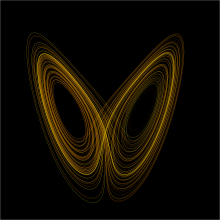
在動力系統中有所謂狀態的概念，是一組可確定的實數。這組實數也是一種流形的幾何空間坐標。動力系統的演化規則是一組函數的固定規律，描述了當前狀態會如何產生未來狀態。這種規則是確定的，即對於給定的時間間隔內，從現在的狀態只能演化出一個未來的狀態。不過也有隨機的系統，因為隨機事件也會影響狀態變量的演化。

若只是在一系列不連續的時間點考察系統的狀態，則這個動力系統為離散動力系統；若時間連續，就得到一個連續動力系統。如果系統以一種連續可微的方式依賴於時間，我們就稱它為一個光滑動力系統。 物理學中的動力系統被描述為「狀態隨時間變化，並因此服從涉及時間導數的微分方程的粒子（群）」。要預測系統未來的行為，需要通過計算機模擬實現這些方程式的分析求解或隨時間積分。

對動力系統的研究是動力系統理論的重點，其在數學、物理學、生物學、化學、工程學、經濟學、歷史學和醫學等眾多領域都有應用。動力系統是混沌理論、邏輯斯諦映射動力學、分岔理論、自組裝和自組織過程與混沌邊緣概念的基本組成。

概覽

動力系統的概念源於牛頓力學。與其他自然科學和工程學科一樣，動力系統的演化規則是一種蘊含關係，只給出系統在未來很短時間內的狀態（這關係可能是微分方程、遞推方程或其他時標微積分）。要確定未來所有時刻的狀態，就要多次迭代這關係，每次前進一小步。迭代過程稱為「求解系統」或「積分系統」。若系統可解，則給定初點，便可能確定未來所有時刻的位置，其集合稱作軌跡（trajectory）或軌道（orbit）。

在計算機發明之前，尋找軌道需要複雜的數學技術，且只能針對一小類動力系統。電子計算機上實現的數值方法大大簡化了確定軌跡的過程。

對簡單動力系統來說，有軌跡就夠用了。但大多數動力系統都過於複雜，無法用單個軌跡求解。出現困難的原因主要有：

• 系統只有近似值—系統參數可能不精確，方程中可能缺項。使用的近似值會影響數值解的有效性或相關性。解決方法是引入了穩定性，如李雅普諾夫穩定性或結構穩定性。動力系統的穩定意味着有一類模型或初始條件的軌跡是等效的，比較軌跡確定等價關係的操作隨着穩定性概念的不同而變化。
• 軌跡類型可能比特定的某條軌跡更重要。有些軌跡可能是周期性的，另一些可能會經歷系統的許多不同狀態。在應用中，往往要枚舉這些類別或將系統限制在一個類別中。分類所有軌跡有助於對動力系統進行定性研究，即研究在坐標變化時不變的特性。線性動力系統和有兩個數字描述狀態的系統是動力系統的例子。
• 軌跡作為參數函數的行為可能是應用所需的。隨着參數變化，動力系統可能出現分岔點，動力系統的定性行為會在點上發生變化。例如，可能從周期性運動變為明顯的不規則行為，如流體向湍流的過渡。
• 系統軌跡可能表現得不穩定，如同隨機。這時可能需要很長的軌跡或許多不同軌跡，再計算均值。遍系統的均值十分明確，而對於雙曲系統，已有了更詳細的理解。對動力系統概率方面的理解有助於建立統計力學和混沌理論的基礎。

歷史

許多人視法國數學家及物理學家龐加萊為動態系統的創始者。他發行了兩份現在被譽為經典的專著：天體力學的新方法《天體力學的新方法》（New Methods of Celestial Mechanics，1892–1899）、《天體力學講義》（Lectures on Celestial Mechanics，1905–1910）。專著中，他成功將研究結果應用在三體問題，並詳細研究其狀態（頻率，穩定性等）。作品中也包含龐加萊復現定理（Poincaré recurrence theorem），該定理指出某些系統在經過足夠長但有限的時間之後，將返回到非常接近初始狀態的狀態。

俄羅斯數學家李亞普諾夫發展許多重要的近似方法。他在1899年發展出的方法，使得定義常微分方程組的穩定性是可行的。 他也創造了動態系統穩定性的現代理論。

美國數學家伯克霍夫在1913年證明了龐加萊的最終幾何定理（Last Geometric Theorem），一個三體問題的特殊形況。在1927年，他則發行了《動態系統》（Dynamical Systems）。在1931年，伯克霍夫發現了最使他名留青史的結果，現在稱作遍歷定理。

美國數學家斯梅爾也對動態系統作出重大貢獻。他的貢獻馬蹄映射推動了動態系統重要研究，此外他還勾劃出研究計劃，讓很多研究者實行。

烏克蘭數學家亞歷山大·沙可夫斯基在1964年給出關於離散動力系統的沙可夫斯基定理，此定理的一個含義是，如果實數軸上的離散動態系統具有週期為3的週期點，那麼它必定具有任意週期的週期點。

正式定義

在最一般的意義上，動力系統是多元組(T, X, Φ)，其中T 是幺半群，X是非空集，Φ是函數

$\Phi :U\subseteq (T\times X)\to X$

其中

$\mathrm {proj} _{2}(U)=X$（$\mathrm {proj} _{2}$是第二射影映射）

$\forall x\in X$:

$\Phi (0,x)=x$

$\Phi (t_{2},\Phi (t_{1},x))=\Phi (t_{2}+t_{1},x),$

令$I(x):=\{t\in T:(t,x)\in U\}(\forall x\in X)$，$\,t_{1},\,t_{2}+t_{1}\in I(x)$、$\ t_{2}\in I(\Phi (t_{1},x))$。

特別地，若$U=T\times X$，則$\forall x\in X$：$I(x)=T$，因此Φ定義了T在X上的幺半群作用。

Φ(t,x)是動力系統的演化函數，將集合X中的點x與唯一的像聯繫起來，取決於變量t，即演化參數。X稱作相空間或狀態空間，而變量x則代表系統的初始狀態。

一般記

$\Phi _{x}(t)\equiv \Phi (t,x)$

$\Phi ^{t}(x)\equiv \Phi (t,x)$

兩個變量之一往往取常數。函數

$\Phi _{x}:I(x)\to X$

稱為過x的流，其圖形稱為過x的軌跡。集合

$\gamma _{x}\equiv \{\Phi (t,x):t\in I(x)\}$

稱為過x的軌道。 注意，過x的軌道是過x的流的像。 若$\forall x\in S,\ \forall t\in T$：

$\Phi (t,x)\in S.$

則狀態空間X的子集S稱為Φ-不變量，特別地，若S是Φ-不變量，那麼$\forall x\in s,\ I(x)=T$。也就是說，對S中每個元素，過x的流必須在所有時刻都有定義。

更常見的動力系統定義有兩類：一種受常微分方程啟發，具有幾何性質；另一種受遍歷理論啟發，具有測度論性質。

幾何定義

幾何定義中，動力系統是多元組$\langle {\mathcal {T}},{\mathcal {M}},f\rangle$。${\mathcal {T}}$是時域——有很多選擇，一般是實數或複數，可能限制為非負。${\mathcal {M}}$的連續情形是流形，即局部為巴拿赫空間或歐氏空間，離散情形是圖。f是演化規則t → f ^t（$t\in {\mathcal {T}}$），使f ^t是流形到自身的微分同胚。所以，f是時域${\mathcal {T}}$到流形到自身的微分同胚空間的「光滑」映射。換句話說，對時域${\mathcal {T}}$內的每一時刻t，f(t)都是微分同胚。

實動力系統

實動力系統、實時動力系統、連續時間動力系統或流是多元組(T, M, Φ)，其中$T\in \mathbb {R}$是開區間，M是局部微分同胚於巴拿赫空間的流形，Φ是連續函數。若Φ還可微，則稱系統是可微動力系統。若流形M局部微分同胚於Rⁿ，則稱系統有限維；否則稱系統無限維。注意，這並不假定存在辛結構。T取實數時，系統稱為流；若T還限制為非負，則系統是半流（semi-flow）。

離散動力系統

離散動力系統、離散時間動力系統是多元組(T, M, Φ)，其中M是局部微分同胚於巴拿赫空間的流形，Φ是函數。T取整數時，系統稱為級（cascade）或映射（map）；若T還限制為非負，則系統是半級（semi-cascade）。

元胞自動機

元胞自動機是多元組(T, M, Φ)，其中T是格子，如整數或更高維的整格；M是從整格到有限集的函數；Φ是（局部定義的）演化函數。這樣，元胞自動機也是動力系統。M中的格子代表「空間」格，T中的格子代表「時間」格。

多維推廣

動力系統通常定義在時間這一單一自變量上。更普遍的一類系統定義在多個自變量上，稱為多維系統，適用於建模，例如數字圖像處理。

動力系統的緊化

給定局部緊豪斯多夫拓撲空間X上的全局動力系統(R, X, Φ)，研究Φ到X的單點緊化X*的連續擴張Φ*通常是有用的。雖然失去了原系統的微分結構，但現在我們可以利用緊性來分析新系統(R, X*, Φ*)。

在緊動力系統中，任何軌道的極限集都是非空單連通緊空間。

測度論定義

主條目：保測動力系統

動力系統可正式定義為一個測度空間的保測變換，即三元組(T, (X, Σ, μ), Φ)。其中T是幺半群（往往是非負整數），X是集合，(X, Σ, μ)是概率空間，即Σ是X上的σ-代數，μ是(X, Σ)上的有限測度。現有映射Φ: X → X，當且僅當$\forall \sigma \in \Sigma$都有$\Phi ^{-1}\sigma \in \Sigma$，稱Φ是Σ-可測函數。當且僅當$\forall \sigma \in \Sigma$都有$\mu (\Phi ^{-1}\sigma )=\mu (\sigma )$，稱映射Φ保測。綜上所述，映射Φ是X 的保測變換，若它是X到自身的Σ-可測、保測變換。三元組(T, (X, Σ, μ), Φ)中的Φ有這樣的性質時，形成了動力系統。

映射Φ體現了動力系統隨時間的演化。因此，離散動力系統研究了每個整數n的迭代函數$\Phi ^{n}=\Phi \circ \Phi \circ \dots \circ \Phi$；連續動力系統的映射Φ被理解為有限時間演化映射，構造更為複雜。

與幾何定義的關係

測度論定義假定存在保測變換。任一演化規則可能都關聯於許多不同的不變測度。若動力系統由微分方程給出，則必須確定適當的測度，這使得由微分方程出發發展遍歷理論變得困難。因此，在遍歷理論中給出以動力系統為動機的定義就變得很方便，這可以避開選擇測度，假定測度已選好。簡單的構造（有時稱為克雷洛夫–博戈柳博夫定理）表明，對一大類系統來說，總可以構造出一類測，使動力系統的演化規則成為保測變換。在構造中，狀態空間的給定測度是軌跡所有未來點的總和，從而確保了不變性。

部分系統有自然測度，如哈密頓系統中的劉維爾定理，是在其他不變測度（如哈密頓系統周期軌道支持的測度）的基礎上選出的。對於混沌耗散系統，不變測度的選擇在技術上更有挑戰性：測度需在吸引子上得到支持，但吸引子的勒貝格測度為0，因此不變測度必須是關于勒貝格測度的奇異測度。這意味着，在演化過程中，相空間的小片區域會收縮。

對於雙曲動力系統，西奈–呂埃勒–鮑恩測度似乎是自然的選擇。它們建立在動力系統穩定流形與不穩定流形的幾何結構上；在微擾下具有物理行為；可以解釋許多觀察到的雙曲系統統計量。

動力系統的構建

正如前幾節所述，「隨時間演化」的思想是動力系統理論的核心，因為理論的初始動機來自經典力學系統的時間行為研究。但常微分方程系統在成為動力系統之前要先求解，例如，考慮以下初值問題：

${\dot {\boldsymbol {x}}}={\boldsymbol {v}}(t,{\boldsymbol {x}})$

${\boldsymbol {x}}|_{t=0}={\boldsymbol {x}}_{0}$

其中

• ${\dot {\boldsymbol {x}}}$表示材料點x的速度
• M是有限維流形
• v: T × M → TM是Rⁿ或Cⁿ中的向量場，且表示相空間M中作用於給定材料點的已知力引起的速度變化。這種變化不是相空間M，而是切空間TM中的矢量。

方程中不需要高階導數，也不需要v(t,x)中的參數t，因為它們都可通過考慮更高維的系統來消除。

根據這一向量場的特性，動力系統可稱為

• 自治的，有v(t, x) = v(x)
• 同類的，對所有t有v(t, 0) = 0

解可用標準常微分方程技術求得，並表為上述演化函數

${\boldsymbol {x}}(t)=\Phi (t,{\boldsymbol {x}}_{0})$

則動力系統就是(T, M, Φ)。

對上述微分方程系進行一些形式化處理，可得到動力系統必須滿足的更一般的方程形式

${\dot {\boldsymbol {x}}}-{\boldsymbol {v}}(t,{\boldsymbol {x}})=0\qquad \Leftrightarrow \qquad {\mathfrak {G}}\left(t,\Phi (t,{\boldsymbol {x}}_{0})\right)=0$

其中${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$是從演化函數集到複數域的函數。 這個方程在模擬具有複雜約束條件的機械系統時非常好用。

動力系統中的許多概念都可擴展到無限維流形（即局部巴拿赫空間），這時微分方程就是偏微分方程。

例子

• 阿諾德貓圖
• 貝克爾圖是混沌分段線性映射的例子
• 檯球動力學
• 彈球模型
• 復二次多項式
• 雙擺
• 二值變換
• 厄農映射
• 無理旋轉
• 卡普蘭–約爾克映射
• 混沌映射列表
• 洛倫茨吸引子
• 若斯叻吸引子
• 擺動阿特伍德機
• 帳篷映射

線性動力系統

主條目：線性動力系統

線性動力系統可用簡單的函數求解，也可對所有軌道的行為進行分類。線性系統的相空間是N維歐氏空間，所以相空間中的點都可用由N個數組成的矢量來表示。線性系統的分析之所以可行，是因為它們滿足疊加原理：若u(t)、w(t)滿足向量場的微分方程（但不一定滿足初始條件），那麼u(t) + w(t)也將如此。

流

對一個流，向量場v(x)是相空間中位置的仿射函數，即

${\dot {x}}=v(x)=Ax+b,$

其中A是矩陣，b是數字向量，x是位置向量。系統的解可通過疊加原理（線性）找到。 b ≠ 0、A = 0的情形只是沿b方向的直線：

$\Phi ^{t}(x_{1})=x_{1}+bt.$

b=0、A ≠ 0時，原點是流的平衡點（或奇異點），即若x₀ = 0，則軌道將保持在附近。 對其他初始條件，運動方程由矩陣指數給出：對於初點x₀，

$\Phi ^{t}(x_{0})=e^{tA}x_{0}.$

b = 0時，A的特徵值決定了系那個空間的結構。根據A的特徵值和特徵向量可以確定初點向原點的平衡點的斂散性。

A ≠ 0時，不同初始條件間的距離在大多數時候呈指數變化，或以指數速度收斂到某點，或以指數速度發散。發散時，線性系統表現出對初始條件的依賴。對非線性系統，這是混沌行為的（必要但非充分）條件之一。

線性向量場和一些軌跡。

映射

離散時間仿射動力系統有矩陣差分方程形式：

$x_{n+1}=Ax_{n}+b,$

其中A是矩陣，b是向量。與連續情形一樣，坐標系變換x → x + (1 − A) ^–1b可以去除方程中的b項。新坐標系的原點是映射的定點，解是線性系統A ⁿx₀的解。 映射的解不再是曲線，而是在相空間中跳躍的點。軌道由曲線或纖維組成，是在映射作用下映射到自身的點集。

與連續情形一樣，A的特徵值和特徵向量決定了相空間的結構。例如，若u₁是A的一個特徵向量，且實特徵值小於1，則沿α u₁(α ∈ R)的點構成的直線就是映射的一條不變曲線，直線上的點都會進入定點。

還有許多其他離散動力系統。

局部動力系統

動力系統的定性特性在坐標的平滑變化下不變（有時這就是定性的定義）：向量場的奇異點（v(x) = 0）在光滑變換下仍是奇異點；周期軌道在相空間和相空間的平滑變形中都是環。在奇異點和周期軌道附近，可以很好理解動力系統相空間的結構。動力系統定性研究的方法是證明存在坐標變化（通常未指定，但可計算），使動力系統儘可能簡單。

整流

相空間大部分小塊區域的流可以變得非常簡單。若y是使向量場v(y) ≠ 0的點，就可以對y附近的坐標進行變換，使向量場變成一系列相同的平行向量。這就是所謂整流定理。

整流定理表明，遠離奇點的小區域中，點的動力特性是直線。小區域可以拼接以擴大，應用於整個相空間M時，稱動力系統可積。小區域一般不能擴展到整個相空間，向量場中可能存在奇點（滿足v(x) = 0的點）；或當接近某點時，區域會變小。更微妙的原因是全局約束，軌跡始於一個區域，途經其他區域後回到原區域。若下次的軌跡以不同方式環繞相空間，就不可能整流整個區域系中的向量場。

近周期軌道

一般來說，周期軌道附近無法應用整流定理。龐加萊提出了一種方法，將周期軌道附近的分析轉化為對映射的分析：擇軌道γ中一點x₀，考慮相空間鄰域中垂直於v(x₀)的點，它們就是軌道的龐加萊截面S(γ, x₀)。現在，流定義了龐加萊映射F : S → S。不是所有點都以相同時間返回，不過時間將接近x₀所需時間。

周期軌道和龐加萊截面的交點是龐加萊映射F的定點。由平移，可假設該點位於x = 0處。映射的泰勒級數是F(x) = J · x + O(x²)，因此改變坐標h只能將F簡化為線性部分

$h^{-1}\circ F\circ h(x)=J\cdot x.$

即所謂共軛方程。尋找方程成立的條件是動力系統研究的主要任務之一。龐加萊首先假設，所有函數都是解析的，並在過程中發現了非共振條件。若λ₁, ..., λ_ν是J的特徵值，且其中1個是其他特徵值的整值線性組合，那麼將是共振的。由於λ_i – Σ（其他特徵值的倍數）形式的項出現在函數h項的分母中，因此非共振條件也被稱為小除數問題 （small divisor problem）。

共軛結果

共軛方程解的存在性結果取決於J的特徵值和h要求的平滑度。由於J不需要任何特殊對稱性，其特徵值通常是複數。J的特徵值不在單位圓上時，F的定點x₀附近的動力稱為雙曲的；特徵值在單位圓上時，動力稱為橢圓的。

前一種情形下，哈德曼–格羅布曼定理給出了存在連續函數的條件，其將映射的定點鄰域映射為線性映射J · x，因此是結構穩定的。向量場的微小變化只會導致龐加萊映射的微小變化，將反映在J的特徵值在複平面的微小位置變化上，意味着龐加萊映射仍是雙曲的。

KAM理論給出了橢點附近的行為。

分岔理論

主條目：分岔理論

演化映射Φ^t（或由其導出的向量場）取決於參數μ時，相空間結構也將取決於該參數。達到特殊值μ₀之後，微小變化可能使相空間發生定性變化，稱動力系統發生了分岔。

分岔理論考慮相空間中的結構（通常是定點、周期軌道或定環面），研究其作為參數μ的行為。結構的穩定性可能在分岔點發生變化，分裂為新的結構，或與其他結構合併。用泰勒級數近似映射、理解坐標變換可能消除的差異，可以對動力系統的分岔點進行編目。

系統族F_μ 的雙曲不動點x₀的分岔可用在分岔點計算的系統一階導數DF_μ(x₀)的特徵值來表徵。對映射而言，當單位圓上存在DF_μ 的特徵值時，就會出現分岔。對流而言，當虛軸上存在更多特徵值時，就會出現分岔。詳見分岔理論條目。

有些分岔會導致相空間出現非常複雜的結構。例如，Ruelle–Takens情形描述了周期軌道如何分岔為環面，環面如何分岔為奇異吸引子。又如，費根鮑姆倍周期描述了穩定的周期軌道如何經歷一系列倍周期分叉。

遍歷系統

主條目：遍歷理論

許多動力系統中，可以選擇合適系統坐標，使相空間中的體積（實際上是ν維體積）不變。只要坐標是位置和動量，體積以（位置）×（動量）為單位，牛頓定律衍生的機械系統就會出現這種情況。流將子集A的點代入Φ ^t(A)，則相空間的不變性意味着

$\mathrm {vol} (A)=\mathrm {vol} (\Phi ^{t}(A)).$

在哈密頓力學中，給定坐標就有可能推導出適當的（廣義）動量，使相關的體積保留在流中。可以說，體積是通過劉維爾測度計算出來的。

哈密頓系統中，並非所有可能的位置和動量構型都能從初始條件得到。由於能量守恆，只有與初始能量相同的狀態才能得到。能量相同的狀態形成一個能殼Ω，是相空間的子流形，體積用劉維爾測度計算，在演化過程中不變。

對於流可保積的系統，龐加萊提出了龐加萊復現定理：假定相空間具有有限的劉維爾體積，並令F為相空間的保積映射，A為相空間的子集。那麼A的幾乎每個點都將無數次返回A。龐加萊復現定理被恩斯特·策梅洛用來反對路德維希·玻爾茲曼對原子碰撞動力系統中熵增的推導。

玻爾茲曼的研究提出的問題之一是時間平均值和空間平均值之間可能存在的等價關係，他稱之為遍歷假說：典型軌跡在區域A中耗費的時長為vol(A)/vol(Ω)。

結果表明，遍歷假說不是統計力學發展多許的基本性質，於是又引入了一系列類遍歷的性質，以捕捉物理系統的相關方面。Koopman利用泛函分析研究遍歷系統。可觀測值a是函數，將相空間的點與數字（如瞬時壓力或平均高度）聯繫起來。利用演化函數φ ^t可計算另一時刻的觀測值，這就引入了轉移算子U ^t：

$(U^{t}a)(x)=a(\Phi ^{-t}(x)).$

研究西那行算子U的譜性質，可對Φ ^t的遍歷性進行分類。用Koopman方法考慮流對可測函數的作用時，涉及Φ ^t的有限維非線性問題便被映射為涉及U的無限維線形問題。

限制在能殼Ω上的劉維爾測度是平衡統計力學中計算平均值的基礎。沿軌跡的時間平均值等同於用玻爾茲曼因子exp(−βH)計算的空間平均值，西奈、呂埃勒和鮑恩（SRB）將這一思想推廣到耗散系統等更大一類動力系統。SRB測度取代了玻爾茲曼因子，是在混沌系統的吸引子上定義的。

非線性動力系統與混沌

主條目：混沌理論

簡單非線性動力系統，甚至分段線性系統都可能表現出完全不可預測（雖然根本上是確定的，但可能表現得隨機）的行為，這種看似不可預測的行為，稱為混沌。雙曲系統是一種定義精確的動力系統，具有混沌系統的特性，垂直於軌跡的切空間可很好地分為兩部分：一部分的點向軌道靠攏（穩定流行），另一部分則偏離（不穩定流形）。

這一數學分支研究動力系統的長期定性行為，重點不是尋找動力系統方程的精確解（一般找不到），而是回答「系統是否會長期穩定，如果是，有哪些可能的吸引子？」或「系統的長期行為是否取決於初始條件？」等問題。

注意複雜系統的混沌行為也不是問題的關鍵——氣象學涉及複雜甚至混沌行為已有多年。混沌理論之所以如此令人驚訝，是因為在幾乎最平凡的系統中也能發現混沌：邏輯斯諦映射只是二次多項式，馬蹄映射只是分段線性函數。

有限時間解

對於非線性自治常微分方程，某些條件下有可能形成有限時間解，這意味着從其自身動力來看，系統將在某時刻達到零值，並永遠保持零值。這種有限持續時間的解不可能是整個實線上的解析函數，由於它們在結束時間是非利普希茨函數，因此不是利普希茨微分方程的唯一解。

例如，方程：

$y'=-{\text{sgn}}(y){\sqrt {|y|}},\,\,y(0)=1$

接受有限時間解：

$y(x)={\frac {1}{4}}\left(1-{\frac {x}{2}}+\left|1-{\frac {x}{2}}\right|\right)^{2}$

另見

• 混沌理論
• 洛倫茲系統
• 複變動態系統
• 線性動態系統

• 行為模型

• 認知模型
• 復變動態系統
• 復變動態系統理論
• 震盪
• 沙可夫斯基定理
• 系統動力學
• 一般系統理論
• 最大徑原理

參考書籍

• Geometrical theory of dynamical systems Nils Berglund's lecture notes for a course at ETH at the advanced undergraduate level.
• Dynamical systems（頁面存檔備份，存於網際網路檔案館）. George D. Birkhoff's 1927 book already takes a modern approach to dynamical systems.
• Chaos: classical and quantum. An introduction to dynamical systems from the periodic orbit point of view.
• Introduction to Social Macrodynamics （頁面存檔備份，存於網際網路檔案館）. Mathematical models of the World System development
• Differential Equations, Dynamical Systems, and an Introduction to Chaos 微分方程、動力系統與混沌導論

延伸閱讀

Works providing a broad coverage:

• Ralph Abraham and Jerrold E. Marsden. Foundations of mechanics. Benjamin–Cummings. 1978. ISBN 0-8053-0102-X.  (available as a reprint: ISBN 0-201-40840-6)
• Encyclopaedia of Mathematical Sciences (ISSN 0938-0396) has a sub-series on dynamical systems with reviews of current research.
• Christian Bonatti; Lorenzo J. Díaz; Marcelo Viana. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective. Springer. 2005. ISBN 3-540-22066-6. 
• Stephen Smale. Differentiable dynamical systems. Bulletin of the American Mathematical Society. 1967, 73 (6): 747–817. doi:10.1090/S0002-9904-1967-11798-1. 

Introductory texts with a unique perspective:

• V. I. Arnold. Mathematical methods of classical mechanics. Springer-Verlag. 1982. ISBN 0-387-96890-3. 
• Jacob Palis and Welington de Melo. Geometric theory of dynamical systems: an introduction. Springer-Verlag. 1982. ISBN 0-387-90668-1. 
• David Ruelle. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. 1989. ISBN 0-12-601710-7. 
• Tim Bedford, Michael Keane and Caroline Series, eds.. Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press. 1991. ISBN 0-19-853390-X. 
• Ralph H. Abraham and Christopher D. Shaw. Dynamics—the geometry of behavior, 2nd edition. Addison-Wesley. 1992. ISBN 0-201-56716-4. 

Textbooks

• Kathleen T. Alligood, Tim D. Sauer and James A. Yorke. Chaos. An introduction to dynamical systems. Springer Verlag. 2000. ISBN 0-387-94677-2. 
• Oded Galor. Discrete Dynamical Systems. Springer. 2011. ISBN 978-3-642-07185-0. 
• Morris W. Hirsch, Stephen Smale and Robert L. Devaney. Differential Equations, dynamical systems, and an introduction to chaos. Academic Press. 2003. ISBN 0-12-349703-5. 
• Anatole Katok; Boris Hasselblatt. Introduction to the modern theory of dynamical systems. Cambridge. 1996. ISBN 0-521-57557-5. 
• Stephen Lynch. Dynamical Systems with Applications using Maple 2nd Ed.. Springer. 2010. ISBN 0-8176-4389-3. 
• Stephen Lynch. Dynamical Systems with Applications using Mathematica. Springer. 2007. ISBN 0-8176-4482-2. 
• Stephen Lynch. Dynamical Systems with Applications using MATLAB 2nd Edition. Springer International Publishing. 2014. ISBN 3319068199. 
• James Meiss. Differential Dynamical Systems. SIAM. 2007. ISBN 0-89871-635-7. 
• David D. Nolte. Introduction to Modern Dynamics: Chaos, Networks, Space and Time. Oxford University Press. 2015. ISBN 978-0199657032. 
• Julien Clinton Sprott. Chaos and time-series analysis. Oxford University Press. 2003. ISBN 0-19-850839-5. 
• Steven H. Strogatz. Nonlinear dynamics and chaos: with applications to physics, biology chemistry and engineering. Addison Wesley. 1994. ISBN 0-201-54344-3. 
• Teschl, Gerald. Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. 2012 [2017-08-24]. ISBN 978-0-8218-8328-0. （原始內容存檔於2012-06-26）. 
• Stephen Wiggins. Introduction to Applied Dynamical Systems and Chaos. Springer. 2003. ISBN 0-387-00177-8. 

Popularizations:

• Florin Diacu and Philip Holmes. Celestial Encounters. Princeton. 1996. ISBN 0-691-02743-9. 
• James Gleick. Chaos: Making a New Science. Penguin. 1988. ISBN 0-14-009250-1. 
• Ivar Ekeland. Mathematics and the Unexpected (Paperback). University Of Chicago Press. 1990. ISBN 0-226-19990-8. 
• Ian Stewart. Does God Play Dice? The New Mathematics of Chaos. Penguin. 1997. ISBN 0-14-025602-4. 

外部連結

• 動態系統介紹 （頁面存檔備份，存於網際網路檔案館）
• Dynamical systems at SUNY：紐約州立大學石溪校區研究小組的網站，有會議、研究者和未解決問題等資料（英）
• Oliver Knill（頁面存檔備份，存於網際網路檔案館）：以JavaScript說明一些動態系統的例子（英）
• Arxiv preprint server（頁面存檔備份，存於網際網路檔案館）：關於此範疇每日的新論文（英）
• Chaos @ UMD（頁面存檔備份，存於網際網路檔案館）：主攻應用層面（英）
• 動態系統的穩定性分析