维基百科

干涉測量術

（重定向自干涉法）

干涉测量术[1][2]（英語：interferometry）又稱干涉量度學，簡稱干涉術、干涉法，是通过由波的叠加（通常为电磁波）引起的干涉现象来获取信息的技术[3]；其将载有被测物信息的探测光与参考光干涉，形成空域或者时域干涉条纹，从而实现光传感、光学计量和各种光学测试技术。例如：进行精密距离和时间的测量。

图一：迈克耳孙干涉仪中的光路。两束由同一光源发出的光在半镀银镜汇合。三个镜子间的距离会影响两束光在汇聚时的相位关系，产生相长或相消条纹。

干涉術这项技术对于天文学、光纤、工程计量、光学计量、海洋学、地震学、光谱学及其在化学中的应用、量子力学、核物理学、粒子物理学、 等离子体物理学、遥感、生物分子间的相互作用（英语：Interactome）、表面轮廓分析、微流控、应力与应变的测量、测速以及验光等领域的研究都非常重要。[4]:1–2

干涉仪（interferometer）广泛应用于科学研究和工业生产中对微小位移、折射率以及表面平整度的测量。在干涉仪中，从单个光源发出的光会分为两束，经不同光路（英语：Optical path），最终交汇产生干涉。所产生的干涉图纹能够反映两束光的光程差。在科学分析中，干涉仪用于测量长度以及光学元件的形状，精度能到纳米级。它们是现有精度最高的长度测量仪器。在傅里叶变换光谱学中，干涉仪用于分析包含与物质相互作用发生吸收或散射信息的光。天文学干涉仪（英语：astronomical interferometer）由两个及以上的望远镜组成，它们的信号汇合在一起，结果的分辨率与直径为元件间最大间距的望远镜的相同。

基本原理

编辑
 
图二：迈克耳孙干涉仪中图纹的形成。
 
图三：迈克耳孙干涉仪产生的彩色与单色干涉纹： a图为倒相数不同的两束白光形成的条纹，b图则为倒相数相同的两束白光形成的条纹，c图为单色光（钠D线）形成的条纹。
更多信息：干涉 (物理学)和迈克耳孙干涉仪

依据叠加原理，波汇合的结果具有能够反映波原始状态的性质。干涉测量术正是基于这一点。当两束频率相同的光叠加时，它们产生的条纹取决于它们的相位差：相位相同时会产生增强条纹，相反则会产生减弱条纹。两种情况之间则会产生中间强度的条纹。这些条纹可以用来分析这两束波的相对相位关系。绝大多数的干涉仪利用的是可见光等电磁波。[4]:3–12

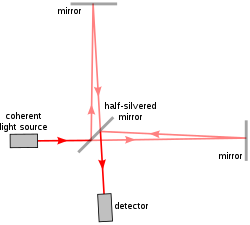
单束入射相干光在干涉仪（如图一中的迈克耳孙干涉仪）中会经过分光镜分为两束。这两束光在到达探测器重新汇聚前会各自经过不同的路径，即光路。光路的不同会导致它们相位产生差异。干涉条纹正是产生于由此引入的相位差。[4]:14–17如果单束光分为两路，这两路光的相位差就可以表征任何可能影响它们光程的因素。这些因素包括路径长度的改变或是路径上折射率的变化。[4]:93–103

图二中，当观察者透过分光镜观察反射镜M1时，可以看到反射镜M2的像M'2。所产生的图纹可以解释为光源S的两个虚像S'1和S'2所发出的光而产生的干涉纹。干涉纹的特征取决于光源的性质以及反射镜与分光镜的具体朝向。在图二a中，光学元件的朝向使得S'1与S'2在观察者眼前排成一线，所产生的干涉纹则为圆心位于M1和M'2法线上的一组同心圆。而当M1和M'2之间如在图二b那样存在一定倾角时，干涉纹则会变为双曲线形，而在 M1和M'2重叠时，轴向附近的图纹会变为彼此平行、均匀分布的直线。而当S不是图中的点光源，而是具有一定空间外延的光源时，图二a中的图纹则需要在无限远处才能观察到，而图二b中的图纹则位于反射镜上。[4]:17

当使用白光时，干涉仪则会产生如图三中的彩色图纹。[4]:26中心的条纹在光程相同时产生。其或亮或暗取决于两束光在光学系统中传播时所经历的倒相次数。[4]:26,171–172

分类

编辑

干涉仪与干涉测量术可以依据以下原则分类：

零差检测与外差检测

编辑

零差检测使用的是波长相同的两束波。它们的相位差会导致检测仪上光强的变化。这种检测涉及两束光汇合后光强的测量以及干涉纹样式的记录。[5]本条目中的干涉仪绝大多数属于此类。

外差检测用于改变输入信号的频率范围或增强输入信号（通常会用到主动混流器（英语：Electronic mixer））。频率为f1的较弱的输入信号会和频率为f2的产生自本地振荡器（英语：Local Oscillator）的较强的参考信号混合在一起。这种非线性的混合会产生两个新信号，一束的频率为两束输入信号频率之和f1 + f2，另一束的频率则为两束输入信号的频率差f1 − f2。这些新频率称作外差。通常检测只会用到其中一种频率，另一束则会自混流器输出时被过滤掉。输出信号的强度与输入信号的振幅之积成比例。[5]

外差技术最为广泛而重要的应用时美国工程师埃德温·霍华德·阿姆斯特朗于1918年发明的超外差收音机。在这种收音机的电路中，由天线接收到的射频信号会与本地振荡器产生的信号混流，然后通过外差技术转换为较低的中频信号。之后这个中频信号会经放大以及滤波，由检波器（英语：detector (radio)）从中提取出音频信号输送到扬声器。[6]光学外差检测（英语：Optical heterodyne detection）是外差技术向可见光频段的延伸。[5]

双光路与共光路

编辑
参见：共光路干涉仪
 
图四：四种共光路干涉仪

在双光路干涉仪中，参考光束与待检光束沿各自的光路传播。迈克耳孙干涉仪、特怀曼-格林干涉仪（英语：Twyman-Green interferometer）、马赫-曾德尔干涉仪皆属此类。待检光束与样品相互作用后，再和参考光束重新汇合产生用以分析的干涉图纹。[4]:13–22

共光路干涉仪（英语：common path interferometer）中则是参考光束与样本光束在共同的光路传播。图4展示了萨奈克干涉仪（英语：Sagnac effect）、光纤陀螺仪、点衍射干涉仪（英语：point diffraction interferometer）以及横向剪切干涉仪（英语：Shearing interferometer）这四种共光路干涉仪。这类干涉仪还有泽尼克相衬显微镜、菲涅耳双棱镜、零面积萨奈克干涉仪及散射板这几类。[7]

波前分割与波幅分割

编辑

波前分割干涉仪会在一个点或一条狭缝分割波前（可以理解为将一束光分割为两束空间相干光），之后让波前的这两个部分分别经不同光路传播之后再汇合。[8]图五展示了杨氏干涉和劳埃德镜这两种波前分割机制。波前分割还有菲涅尔双棱镜、比耶（Billet）双透镜以及瑞利干涉仪（英语：Rayleigh interferometer）这几种机制。[9]

 
图五：两种波前分割机制

1803年进行的杨氏干涉实验在光的波动理论为公众接受的过程中举足轻重。如果实验中使用的是白光的话，干涉结果中心会是由相长干涉（由于两束干涉光的光路相同）造成的白色光带，两侧则是亮度逐渐降低的对称彩色光带。除了连续的电磁辐射外，单光子以及电子间也会发生杨氏干涉。[10][11][12]电子显微镜能够观测到的巴基球同样也能杨氏干涉。[13]

劳埃德镜中则是由光源与光源的掠射像发出的光（分别是图中的蓝线与红线）发生干涉。所产生的干涉纹并不对称。离反射镜最近的由同光路产生的光带却并不是亮的而是暗光带。汉弗莱·劳埃德在1834年通过这个效应证明了前表面反射光束的相位发生反转的现象。[14][15]

波幅分割干涉仪则利用部分反射镜通过分割待测光波波幅将其分为几束，然后在重新汇聚。图六展示了斐索干涉仪（英语：Fizeau interferometer）、 马赫－曾德尔干涉仪以及法布里－佩罗干涉仪。波幅分割干涉仪还有迈克耳孙干涉仪、特怀曼-格林干涉仪（英语：Twyman–Green interferometer）、激光不等光程干涉仪以及林尼克干涉仪（英语：Linnik interferometer）几种。[16]

 
图六：三种波幅分割干涉仪：斐索干涉仪、马赫-曾德尔干涉仪以及法布里-佩罗干涉仪

斐索干涉仪可以用于检测光学平面（英语：optical flat）。一个参考平面放在待检平面之上。两个平面之间有狭小的空隙。参考平面上表面稍稍倾斜（倾斜角在一度之内）避免后表面的干扰。待检平面与参考平面间的空隙使得两个平面可以成一定的倾角。这个倾角可以增添一个可控的相位梯度以形成干涉纹。人们可以以此来控制干涉纹的排布与方向，得到近乎平行的干涉纹序列而非复杂的轮廓线漩涡。不过平面的分离需要照明光准直。图六展示了一束准直单色光照明两个平面。分束器令干涉纹可以在轴向上观测到。[17][18]

马赫-曾德尔干涉仪相对于迈克耳孙干涉仪来说则更为灵活。每个光路只需走一次即可，而干涉纹也可在随需要在任意平面上产生。[4]:18通常来说，干涉纹会被放在与待测物体相同的平面内，以使两者可以同时被拍摄到。如果要使用白光来产生干涉纹的话，由于其相干长度有限（在微米量级），光路必须精细调整，否则不会产生可见的条纹。如图六所示，参考光束的光路中必须放置补偿单元以与待测单元匹配。同时分束器的朝向也需要精准调节。分束器的反射平面的朝向必须调整至能使待测光束与参考光束通过的玻璃的量相同。这种朝向可使两束光都经历两次前表面反射，以使相位反转数一致。最终两束光的光程相等，产生相长的白光干涉条纹。[19][20]

法布里-佩罗干涉仪的核心是一对部分镀银的玻璃光学平面。两个平面相距几毫米或几厘米的距离，且镀银面相对放置。这个装置可以用具有两个平行反射面的透明的法布里-佩罗标准具代替。[4]:35–36与斐索干涉仪类似，平面需要稍稍倾斜。典型配置中是由放置在凸透镜焦平面的散射光源提供照明。如果另一侧没有对应的平面的话，那么这样放置会使凸透镜产生光源的倒像，也就是说所有从点A发出的穿过光学系统的光会在点A'汇聚。图六中只描绘了从A点发出的一束光的情况。随着光线穿过对应的平面，它会多次反射产生多条透射光，由凸透镜汇集，投射到屏幕上的A'点。整个干涉纹会是一组同心亮环。亮环的锐度取决于平面的反射率。如果反射率较高的话，所得到的结果Q因子也会比较高（也就是说精细度较高），人们将会看到单色光在暗背景上产生一组窄亮环。[21]图六中，精细度较低的图像由反射率为0.04（未镀银的表面）的平面产生，高精细度图像对应的反射率则为0.95。

迈克耳孙和莫雷（1887）[22]以及同时期其他科学家都是用过干涉技术来测定以太的特性。他们在搭建系统时采用的是单色光，在实际测定中使用的则是白光。这是由于测定结果会做图像记录。单色光会产生均匀的干涉纹。尽管干涉仪常在地下室中搭建，然而由于缺乏控制环境温度的有效手段，实验者会时常经历干涉纹的漂移。而马车经过等等产生的震动也会使干涉纹消失。而当干涉纹重新可见时，观察者常陷于迷茫之中。虽然白光较低的相干长度会给仪器的搭建带来麻烦，但瑕不掩瑜，白光能产生鲜明的彩色干涉条纹的特色还是令科学家对其更为青睐。[23]这也是白光用于解决“2 模糊”的早期应用实例。

实际应用

编辑

光学干涉测量

编辑

可见光的干涉测量是干涉测量术中最先发展同时也得到最广泛应用的类别，早期的实际应用如迈克耳孙测星干涉仪对恒星角直径的测量，但如何获取稳定的相干光源始终是限制光学测量发展的重要原因之一。直至二十世纪六十年代，光学干涉测量技术得到了飞速的发展，这要归功於激光这一高强度相干光源的发明[24][25]，计算机等数字集成电路获取并处理干涉仪所得数据的能力大大提升[26]，以及单模光纤的应用增长了实验中的有效光程并仍能保持很低的噪声[27]。电子技术的发展使人们不必再去观察干涉仪产生的干涉条纹，而可以对相干光的相位差直接进行测量。这里列举了光学干涉测量在多个方面的一些重要应用。

长度测量

编辑
 
用於测量光程差改变，进而测定气体折射率的瑞利干涉仪（英语：Rayleigh interferometer）[28][29]。

长度测量是光学干涉测量最常见的应用之一。如要测量某样品的绝对长度，最简明的方法之一是通过干涉对产生的干涉条纹进行计数；若遇到非整数的干涉条纹情形，则可以通过不断成倍增加相干光的波长来获得更窄的干涉条纹，直到得到满意的测量精度为止[30][31]。常见的方法还包括惠普公司研发的惠普干涉仪[32][33]，它通过外加一个轴向磁场使氦－氖激光器 （页面存档备份，存于互联网档案馆）工作在两个相近频率，从而发出频率相差2兆赫兹的两束激光，再通过偏振分束器使这两束激光产生外差干涉。干涉得到的差频信号被光检测器记录，而待测样品引起的光程差变化则可以通过计数器表示为光波长的整数倍。惠普干涉仪可以测量在60米左右以内的长度，在附加其他光学器件后还可以用於测量角度、厚度、平直度等场合。此外，还可以通过声光调制的方法得到差频信号，并且这种方法能获得更高的差频频率，从而可以从差频信号中得到更高的计数。

长度测量的另一类情形是测量长度的变化，常见的方法如借助声光调制产生的外差干涉，差频信号所携带的相位差会被光检测器记录，从而得到长度的变化[34]。在测量像熔凝石英这样热膨胀系数很低的材料的热膨胀系数时，还经常用到一种更精确的方法：将两面部分透射部分反射的玻璃板置于待测样品的两端，从而构成一个法布里－珀罗干涉仪。使用两束发生外差干涉的激光，并通过反馈将其中一束激光的频率锁定到法布里－珀罗干涉仪的一个透射峰值频率上。这样，当样品发生热膨胀而改变法布里－珀罗干涉仪的长度时，透射峰值频率的变化会引起被锁定的激光频率的相应变化，这一变化也会反映到外差信号中从而被探测到[35][36]。

光学检测

编辑
 
剪切干涉仪的光路示意图

光学检测包括对光学元件和光学系统的检查和测试，诸如利用等厚干涉条纹来测量玻璃板各处的厚度，以及测量照相机镜头的调制传递函数（MTF）等都属于这类应用。利用等厚干涉来检测样品表面是否平整的最常见方法是斐索干涉仪[37]，它利用准直平行光在样品表面反射后与入射光发生干涉，从而得到等厚条纹。此外，还可以采用从迈克耳孙干涉仪改进而来的特怀曼－格林干涉仪[38]。特怀曼－格林干涉仪也使用准直平行光源，并由于从迈克耳孙干涉仪改进而来，它可以使两束相干光的光程非常接近，从而相比於斐索干涉仪它对光源的相干长度要求有所降低。

另一类广泛应用於检测光学元件表面、光学系统像差以及测量光学传递函数的干涉仪是剪切干涉仪[39][40]，它将待测样品出射的波前分成两个，并使其相互错开一定距离（这段距离被称作剪切），两个波前重叠的部分即产生干涉图样。剪切干涉仪分为切向剪切、法向剪切和旋转剪切等类型：切向剪切干涉仪通常是一块平行平面板或略呈角度的劈尖，准直光源入射到平行平面板上就形成了两束错开的相干光；而法向剪切干涉仪则类似於斐索干涉仪和特怀曼－格林干涉仪。剪切干涉仪的优点是省去了作为参考的光学表面，结构简单且两束相干光的光程基本相等，而缺点则是对干涉图样的数值分析比较繁琐。

干涉光谱

编辑

光谱仪可分辨的两条谱线的中心波长与恰好可分辨的波长差的比值，称作光谱仪的色分辨本领。对利用色散效应的棱镜光谱仪以及利用衍射效应的光栅光谱仪，其色分辨本领都不会超过106的量级[41]。然而若采用法布里－珀罗干涉仪，由于透射峰的半宽等于干涉仪的自由光谱范围除以它的细度：

 

并由干涉条件 代入可得

 ，其中 是中心频率。

从而法布里－珀罗干涉仪的色分辨本领为 。一般干涉序 ，细度 至少在 ，从而干涉光谱仪的色分辨本领在106至107的量级以上[42]。

干涉仪的另一个重要应用是制造波长计，波长计又分为动态波长计和静态波长计，前者包含活动组件可调节光程差[43][44]，后者则采用光程差为倍数递增关系的多个迈克耳孙干涉仪或自由光谱范围为倍数递增关系的多个法布里－珀罗干涉仪组合而成[45]。此外利用激光的外差干涉，结合法布里－珀罗干涉仪可以更精确地测量激光的频率或比较两束激光的频率高低[46]，并通过声光调制和光纤延迟还可以测量出激光的线宽[47]。

天体测量

编辑
 
位於亚利桑那州的海军原型光学干涉仪

在迈克耳孙测星干涉仪被发明以前，恒星直径的测量始终是天文学上的一个难题，因为已知体积最大的恒星的角直径也只有10-2角秒。然而即使是迈克耳孙测星干涉仪，其分辨率也只能测量某些巨星的角直径，对质量稍小的恒星就无能为力[48]。正是激光和外差干涉技术的发明，自二十世纪七十年代起在测星干涉领域引发了一场革新。在这些经改进的干涉仪中，望远镜捕捉到的星光与本地的激光发生外差干涉，两者频率非常接近，从而产生了射电频域内的拍频信号；并且由于这个拍频信号的光强来自星光和激光光强的乘积，这种干涉从而能获得更高的分辨率[49][50]。此外这些实验大多使用了波长为10.6微米的二氧化碳激光，这也是由于较长的波长能提高外差干涉的分辨率[51]。1974年，约翰森、贝茨和唐尼斯建造了一台基线长度为5.5米的差频干涉仪，使用了功率为1瓦特并经过稳频的二氧化碳激光，其工作波长为10.6微米[52]。他们用这台干涉仪对一系列红外线源进行了观测，包括M型超巨星、米拉变星，并取得了一些星周尘壳的温度和质量分布等信息[53][54]。而今随着技术和制造工艺的进步，这类干涉仪的基线长度已经可以扩展到几百米的距离，从而克服了最初迈克耳孙测星干涉仪遇到的困难[55]。

天体测量学上的另一个问题是关于天体的位置和运动的测量[56][57]。通过对恒星进行精确定位，可以将观测到的射电源位置和它们观测到的相应光学位置进行比对，从而直接测量它们的视差并建立宇宙距离尺度。此外这种测量还能帮助确定双星系统轨道的尺寸和形状。这类干涉仪包括位於亚利桑那州的海军原型光学干涉仪（NPOI）[58]，它由四个基本部分组成Y形，彼此之间的干涉臂长度为20米，NPOI对天体的定位可以达到毫角秒的量级[59]；以及太阳系外行星天文干涉仪（ASEPS-0），它通过监视恒星因围绕其运动的行星而引起的反映运动来研究太阳系外行星[60]。

引力波探测

编辑

引力波是广义相对论所预言的以光速传播的时空扰动，虽然引力波与物质的相互作用非常微弱，但已有间接的天体观测证据表明它确实存在於诸如双星系统这样的天体中，并对这类天体的物理性质有着重要影响。对引力波的直接观测不仅可以验证广义相对论，更重要的是提供了一种有别于基于电磁波观测的传统观测天文学的新观测手段。并且由于电磁波与引力波的不同性质，引力波天文学所研究的将是借助电磁波无法观测到的宇宙的另一个侧面[61]。自二十世纪七十年代起，人们逐渐认识到基于干涉原理的引力波探测器是一种较有希望成功的设计，这类探测器的基本构成都是一架等臂迈克耳孙干涉仪[62][63]：本质上，激光干涉引力波探测器是对干涉臂的长度变化进行测量，并对所观测得的数据进行分析，寄希望於寻找到其中引力波所导致的影响。即引力波所导致的干涉臂长度变化与干涉臂长度的比值：

 

其中 和 是引力波的两个偏振态， 和 是探测器分别对这两个偏振态的响应， 是引力波的应力强度。在实际操作中，来自外界振动、分子热运动、以及光检测器读出的散粒噪声等噪声会叠加到观测数据中，因而对一般来自天体的引力波而言，如要探测到它们要求探测器的灵敏度要优于 并尽可能地降低其他噪声。通过使用较长的干涉臂同时在两端分别增加法布里－珀罗谐振腔[64][65]，以及采用功率回收技术等方法[66][67]，可以有效地降低噪声并提高干涉仪的灵敏度。

 
意大利－法国联合建造的激光干涉引力波探测器VIRGO（局部）

美国路易斯安那州和华盛顿州的激光干涉引力波天文台（LIGO）是典型的基于迈克耳孙干涉仪和法布里－珀罗谐振腔的地面引力波探测器，它被寄希望于探测到频率在20赫兹至10千赫兹范围内的引力波信号[68]。相同架构的地面引力波探测器还有意大利的VIRGO、德国的GEO600，日本的TAMA300以及计划中的LCGT。美国国家航空航天局和欧洲空间局正在合作研发激光干涉空间天线（LISA）项目，计划在太空中进行类似於迈克耳孙干涉仪的激光干涉，对低频区域（30微赫至0.1赫兹）的引力波进行探测[69]。此外，日本正在计划中的分赫兹干涉引力波天文台（DECIGO）同样属于空间计划，人们寄希望於它能够探测分赫兹范围上的引力波，从而填补LIGO和LISA工作频域之间的空白[70]。

射电干涉测量

编辑
主条目：射电天文学
 
甚大天线阵

望远镜的角分辨率正比於波长除以口径，而由于无线电波的波长远长于可见光，这造成单个射电望远镜无法达到观测一般的射电源所需的分辨率（例如采用波长为2.8厘米的无线电波进行分辨率为1毫角秒的观测，需要达6000千米的望远镜口径）。基于这个原因，英国天文学家马丁•赖尔爵士等人於1946年发明了射电干涉技术，他们用一架两根天线组成的射电干涉仪对太阳进行了观测[71]。射电干涉技术采用多个分立的射电望远镜构成阵列，这些望远镜在观测时都对准同一射电发射源，各自观测所得的信号彼此用同轴电缆、波导或光纤连接后发生干涉。这种干涉不仅仅是提升了观测信号的强度，而且由于望远镜彼此间的基线距离很长，从而提升了观测的有效口径。由于各个望远镜的位置不同，同一波前到达各个望远镜的时间因而会存在延迟，这就需要对先到达的信号进行恰当的延迟以保持信号彼此之间的时间相干性。此外，构成干涉的望远镜数量越多越好，这是由于观测射电源表面的光强分布时，两台望远镜组成的干涉只能观测到光强分布的傅立叶变换（即可见度）的各个空间频率（这里空间频率的含义是描述光强在不同方向上变化快慢的傅立叶频率）中的一个频率；而采用多个望远镜构成阵列，则可以在多个空间频率上对射电源进行观测，再对观测所得的可见度函数进行逆傅立叶变换得到射电源的光强分布，这种方法叫做合成孔径[72]。例如，位於新墨西哥州的甚大天线阵（VLA）由27架射电望远镜组成，每架望远镜由直径为25米的抛物面天线构成，彼此共形成351条彼此独立的干涉基线，最长的等效基线可达36千米[73]。

二十世纪六十年代末，随着射电望远镜接收器的性能和稳定性的提高，在全世界（以至地球轨道）范围内使望远镜相距很远的同一射电信号之间产生干涉成为可能，这被称为超长基线干涉（VLBI）[74]。超长基线干涉不需要观测信号之间的物理连接，而是在信号数据本身嵌入被原子钟校准的时间信息，之后再将这些数据进行相关性计算。由于这些数据是在相隔很远的地点观测到的，等效基线能够达到非常之长。现在已经运行的超长基线干涉仪包括位於美国本土及海外领地的超长基线阵列（基线长度8611千米）[75]，以及遍布欧亚和非洲大陆的欧洲超长基线干涉网[76]。这些干涉阵列平时都进行着独立的观测，但在一些特殊项目中可以实现同时性的观测，从而形成全球性的超长基线干涉。

參見

编辑
 
维基共享资源上的相关多媒体资源：干涉測量術

参考文献

编辑
  1. ^ 存档副本. [2024-01-24]. （原始内容存档于2024-01-24）. 
  2. ^ https://terms.naer.edu.tw/detail/b300dd7ca0b216022a11474a2bb26b46/
  3. ^ Bunch, Bryan H; Hellemans, Alexander. The History of Science and Technology. Houghton Mifflin Harcourt. April 2004: 695. ISBN 978-0-618-22123-3. 
  4. ^ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 Hariharan, P. Basics of Interferometry. Elsevier Inc. 2007. ISBN 0-12-373589-0. 
  5. ^ 5.0 5.1 5.2 Paschotta, Rüdiger. Optical Heterodyne Detection. RP Photonics Consulting GmbH. [1 April 2012]. （原始内容存档于2015-03-19）. 
  6. ^ Poole, Ian. The superhet or superheterodyne radio receiver. Radio-Electronics.com. [22 June 2012]. （原始内容存档于2018-08-19）. 
  7. ^ Mallick, S.; Malacara, D. Common-Path Interferometers. Optical Shop Testing. 2007: 97. ISBN 9780470135976. doi:10.1002/9780470135976.ch3. 
  8. ^ Verma, R.K. Wave Optics. Discovery Publishing House. 2008: 97–110 [2018-08-19]. ISBN 81-8356-114-4. （原始内容存档于2019-08-22）. 
  9. ^ Interferential Devices – Introduction. OPI – Optique pour l'Ingénieur. [1 April 2012]. （原始内容存档于2018-08-01）. 
  10. ^ Ingram Taylor, Sir Geoffrey. Interference Fringes with Feeble Light (PDF). Proc. Camb. Phil. Soc. 1909, 15: 114 [2 January 2013]. （原始内容存档 (PDF)于2018-09-24）. 
  11. ^ Jönsson, C. Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Zeitschrift für Physik. 1961, 161 (4): 454–474. Bibcode:1961ZPhy..161..454J. doi:10.1007/BF01342460. 
  12. ^ Jönsson, C. Electron diffraction at multiple slits. American Journal of Physics. 1974, 4: 4–11. Bibcode:1974AmJPh..42....4J. doi:10.1119/1.1987592. 
  13. ^ Arndt, M.; Zeilinger, A. Heisenberg's Uncertainty and Matter Wave Interferometry with Large Molecules. Buschhorn, G. W.; Wess, J. (编). Fundamental Physics-- Heisenberg and Beyond: Werner Heisenberg Centennial Symposium "Developments in Modern Physics". Springer. 2004: 35–52 [2018-08-19]. ISBN 3540202013. （原始内容存档于2022-01-15）. 
  14. ^ Carroll, Brett. Simple Lloyd’s Mirror (PDF). American Association of Physics Teachers. [5 April 2012]. （原始内容存档 (PDF)于2018-09-25）. 
  15. ^ Serway, R.A.; Jewett, J.W. Principles of physics: a calculus-based text, Volume 1. Brooks Cole. 2010: 905–905 [2018-08-19]. ISBN 0-534-49143-X. （原始内容存档于2021-08-06）. 
  16. ^ Nolte, David D. Optical Interferometry for Biology and Medicine. Springer. 2012: 17–26 [2018-08-19]. ISBN 1-4614-0889-X. （原始内容存档于2021-08-06）. 
  17. ^ Guideline for Use of Fizeau Interferometer in Optical Testing (PDF). NASA. [8 April 2012]. （原始内容 (PDF)存档于2018-09-25）. 
  18. ^ Interferential devices – Fizeau Interferometer. Optique pour l'Ingénieur. [8 April 2012]. （原始内容存档于2018-08-30）. 
  19. ^ Zetie, K.P.; Adams, S.F.; Tocknell, R.M. How does a Mach–Zehnder interferometer work? (PDF). Physics Department, Westminster School, London. [8 April 2012]. （原始内容存档 (PDF)于2018-09-25）. 
  20. ^ Ashkenas, Harry I. The design and construction of a Mach-Zehnder interferometer for use with the GALCIT Transonic Wind Tunnel. Engineer's thesis. California Institute of Technology. 1950 [2018-08-19]. （原始内容存档于2019-05-03）. 
  21. ^ Betzler, Klaus. Fabry-Perot Interferometer (PDF). Fachbereich Physik, Universität Osnabrück. [8 April 2012]. （原始内容存档 (PDF)于2018-09-25）. 
  22. ^ Michelson, A.A.; Morley, E.W. On the Relative Motion of the Earth and the Luminiferous Ether (PDF). American Journal of Science. 1887, 34 (203): 333–345 [2018-08-19]. doi:10.2475/ajs.s3-34.203.333. （原始内容存档 (PDF)于2016-03-07）. 
  23. ^ Miller, Dayton C. The Ether-Drift Experiment and the Determination of the Absolute Motion of the Earth. Reviews of Modern Physics. 1933, 5 (3): 203–242. Bibcode:1933RvMP....5..203M. doi:10.1103/RevModPhys.5.203. White light fringes were chosen for the observations because they consist of a small group of fringes having a central, sharply defined black fringe which forms a permanent zero reference mark for all readings. 
  24. ^ Hariharan 2003，第79頁
  25. ^ Hariharan, P. (1987a). In “Progress in Optics” (E.Wolf, ed.),Vol. XXIV, pp. 105–164. Elsevier, Amsterdam.
  26. ^ Hariharan 2003，第93頁
  27. ^ Hariharan 2003，第xiii頁
  28. ^ Hariharan 2006，第15頁
  29. ^ Busch 1990，第231頁
  30. ^ Hariharan 2006，第59頁Hariharan 2003，第106-107頁
  31. ^ Bourdet, G. L., and Orszag, A. G. (1979). Appl. Opt. 18, 225–227.
  32. ^ Hariharan 2006，第59-60頁
  33. ^ J. N. Dukes and G. B. Gordon, Hewlett-Packard Journal 21, No. 12, 2–8, Dec. 1970
  34. ^ Hariharan 2006，第62頁Hariharan 2003，第116-117頁
  35. ^ Hariharan 2006，第63頁Hariharan 2003，第116頁
  36. ^ Jacobs, S. F., and Shough, D. (1981). Appl. Opt. 20, 3461–3463.
  37. ^ Hariharan 2003，第119-121頁Hariharan 2006，第67-69頁
  38. ^ Born 1999，第336-341頁Hariharan 2003，第121-122頁Hariharan 2006，第70-71頁
  39. ^ Hariharan 2003，第124-129頁Hariharan 2006，第73-77頁
  40. ^ Hopkins, H. H. (1955). Opt. Acta 2, 23–29.
  41. ^ Hariharan 2003，第157頁
  42. ^ Hariharan 2003，第159頁
  43. ^ Hariharan 2003，第165-167頁
  44. ^ Kowalski, F. V., Hawkins, R. T., and Schawlow, A. L. (1976). J. Opt. Soc. Am. 66, 965–966.
  45. ^ Hariharan 2003，第167-168頁
  46. ^ Hariharan 2003，第169頁
  47. ^ Hariharan 2003，第169-170頁
  48. ^ Born 1999，第308頁
  49. ^ Hariharan 2003，第227-230頁
  50. ^ Nieuwenhuizen, H. (1970). Mon. Not. Roy. Astron. Soc. 150, 325–335.
  51. ^ Siegman, A. E. (1966). Proc. IEEE 54, 1350–1356.
  52. ^ Johnson, M. A., Betz, A. L., and Townes, C. H. (1974). Phys. Rev. Lett. 33, 1617– 1620.
  53. ^ Sutton, E. C., Storey, J. W. V., Betz, A. L., Townes, C. H., and Spears, D. L. (1977). Astrophys. J. Lett. 217, L97.
  54. ^ Sutton, E. C. (1979). In “High Angular Resolution Interferometry,” Proceedings of Colloquium No. 50 of the IAU, pp. 16/1–16/14. University of Sydney, Sydney.
  55. ^ Tango, W. J., and Twiss, R. Q. (1980). In “Progress in Optics” (E. Wolf, ed.), Vol. XVII, pp. 241–277. North-Holland, Amsterdam.
  56. ^ Hariharan 2003，第235-238頁
  57. ^ Shao, M., and Staelin, D. H. (1977). J. Opt. Soc. Am. 67, 81–86.
  58. ^ NAVY PROTOTYPE OPTICAL INTERFEROMETER. [2015-03-02]. （原始内容存档于2005-02-05）. 
  59. ^ Armstrong, J. T., Mozurkewich, D., Rickard, L. J., Hutter, D. J., Benson, J. A., Bowers, P. F., Elias II, N. M., Hummel, C. A., Johnston, K. J., Buscher, D. F., Clark III, J. H., Ha, L., Ling, L. C., White, N. M., and Simon, R. S. (1998). Astrophys. J. 496, 550–571.
  60. ^ Colavita, M. M., Shao, M., Hines, B. E., Wallace, J. K., Gursel, Y., Malbet, F., Yu, J. W., Singh, H., Beichman, C. A., Pan, X. P., Nakajima, T., and Kulkarni, S. R. (1994). Proc. SPIE 2200, 89–97.
  61. ^ Hariharan 2003，第241-247頁
  62. ^ Moss, G. E., Miller, L. R., and Forward, R. L. (1971). Appl. Opt. 10, 2495–2498.
  63. ^ Weiss, R. (1972). Quart. Prog. Rep. Res. Lab. Electron. M.I.T. 105, 54–76.
  64. ^ Drever, R. W. P., Hough, J., Munley, A. J., Lee, S. A., Spero, R., Whitcomb, S. E., Ward, H., Ford, G. M., Hereld, M., Robertson, N. A., Kerr, I., Pugh, J. R., Newton, G. P., Meers, B., Brooks, E. D., III, and Gursel, Y. (1981). In “Laser Spectroscopy V” (A. R. W. McKellar, T. Oka, and B. P. Stoicheff, eds.), pp. 33–40. Springer-Verlag, Berlin.
  65. ^ Weiss, R. (1999). Rev. Mod. Phys. 71, S187–S196.
  66. ^ Meers, B. J. (1988). Phys. Rev. D 38, 2317–2326.
  67. ^ Fritschel, P., Shoemaker, D., andWeiss, R. (1992). Appl. Opt. 31, 1412–1418.
  68. ^ LIGO Science Requirements Document (SRD) (PDF). [2010-08-24]. （原始内容 (PDF)存档于2006-09-25）. 
  69. ^ LISA Science Requirements Document (SRD) (PDF). （原始内容 (PDF)存档于2016-03-04）. 
  70. ^ The Japanese Space Gravitational Wave Antenna - DECIGO (PDF). （原始内容 (PDF)存档于2010-07-27）. 
  71. ^ Thompson 2001，第12頁
  72. ^ Basics of Radio Interferometry (PDF). [2010-08-25]. （原始内容存档 (PDF)于2008-08-27）. 
  73. ^ National Radio Astronomy Observatory. [2010-08-25]. （原始内容存档于2017-09-13）. 
  74. ^ Thompson 2001，第304頁
  75. ^ National Radio Astronomy Observatory. [2010-08-25]. （原始内容存档于2011-04-08）. 
  76. ^ The European VLBI Network. [2010-08-25]. （原始内容存档于2013-03-16）. 
检索自“https://zh.wikipedia.org/w/index.php?title=干涉測量術&oldid=83909160”