球面像差
球面像差(英語:SA/Spherical aberration),是指發生在經過透鏡折射或面鏡反射的光線,接近中心與靠近邊緣的光線不能將影像聚集在一個點上的現象。這在望遠鏡和其他的光學儀器上都是一個缺點。這是因為透镜和面鏡必须满足所需的形狀,否则不能聚焦在一個點上造成的。 球面像差與鏡面直徑的四次方成正比,與焦長的三次方成反比,所以他在低焦比的鏡子,也就是所謂的「快鏡」上就比較明顯。
對使用球面鏡的小望遠鏡,當焦比低於f/10時,來自遠處的點光源(例如恆星)就不能聚集在一個點上。特別是來自鏡面邊緣的光線比來自鏡面中心的光線更不易聚焦,這造成影像因為球面像差的存在而不能很清晰的成象。所以焦比低於f/10的望遠鏡通常都使用非球面鏡或加上修正鏡。
在透鏡系統中,可以使用凸透鏡和凹透鏡的組合來減少球面像差,就如同使用非球面透鏡一樣。
-
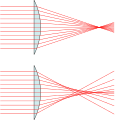
球面像差。一個理想的鏡面(頂端),能經所有入射的光線匯聚在光軸上的一個點,但一個真實的鏡面(底端)會有球面像差:靠近光軸的光線會比離光軸較遠的光線較為緊密的匯聚在一個點上,因此光線不能匯聚在一個理想的焦點上(圖較為誇張)
-
一個 點光源 在負球面像差(上) 、無球面像差(中)、和正球面像差(下)的系統中的成像情形。左面的影像是在焦點內成像,右邊是在焦點外的成像
-
平行光束通過透鏡後聚焦像的縱切面,上:負球面像差,中:無球面像差,下:正球面像差。鏡子位於圖的左側
-
來自球面鏡的球面像差
球面像差公式 编辑
- 单球面
一个球面,PA 为由球面顶点到非近轴光线入射点距离,球面左右介质的折射率分别为n,n';非近轴入射角,折射角分别为J,J';非近轴入射线和折射线与光轴的夹角分别为U,U';近轴光线的入射角为i;这个球面对球面像差的贡献为[1]
球面像差=
在四种情况下,球面像差为零:
- PA=0:物体和像与球面顶点重合;
- I'=I:物体和物象在球面的曲率中心;
- i=0;
- I=U'或I'=U:在这种情形下的球面成为消球差曲面。
- 消球差球面
根据球面折射的基本方程可以导出[2]:
对于消球差曲面,凡是射向同一点B入射光,其折射线与光轴相交于一个共同点B'。
例如,n=1,n'=1.5[3]。
消球差曲面多用于高倍率显微镜的物镜[4][3]。一个消球差薄透镜由一个消球差球面和一个平面镜组成,对于平行光。消球差薄透镜等同一块平板玻璃,对于聚合光束,消球差薄透镜增加光束的聚合度,对于发散光束,消球差薄透镜增加光束的发散度[5]。
- 同轴球面系
对于一个由多个球面组成镜头,球面像差由以下公式给出[6]:
LA'=trans+newsp
其中 trans=
newsp=
| 維基教科書中的相關電子教程:球面像差 |
球面像差展开式 编辑
球面像差可表示为
LA'= ………………[7][8]。其中Y是入射光线的在球面入射点到光轴的距离。
红线代表二次项,蓝线代表二次和四次项之和,黑线为二、四、六次项之和
薄透镜组的球面像差 编辑
亚历山大·尤金·康拉迪推导出薄透镜组的球面像差公式如下[9][10]:
SC= 。
其中“0”代表最后的结果,Σ代表对各镜片之和
薄透镜的球面像差 编辑
对于单薄镜片,上式可简化为[11]。
单镜片的球面像差=LA'=
令上式对c_1的导数为零,可求得单镜片具有最小球面像差的条件[12]:
=
即 = .
当物距为无穷远时,v_1=0;
于是
[13]。
| n | r_1/r_2 |
|---|---|
| 1.5 | -6 |
| 1.518 | -6.7374 |
| 1.6 | -14 |
| 1.7 | 93.5 |
| 1.8 | 12.1765 |
| 2 | 5 |
| 3 | 1.9 |
| 4 | 1.5 |
参考文献 编辑
- ^ Kingslake p104
- ^ Rudolf Kingslake p104-105
- ^ 3.0 3.1 Rudolf Kingslake p105
- ^ Moritz von Rohr p244
- ^ Rudolf Kingslake p106
- ^ Rudolf Kingslake p104
- ^ A.E.Conrady p101
- ^ Kingslake p114
- ^ Alexander Eugen Conrady, p95
- ^ Kingslake p117
- ^ Kingslake p118
- ^ Kingslake, p118
- ^ Kingslake p119
- von Rohr莫里兹·冯·罗尔, Moritz. Geometrical Investigation of the Formation of Images in Optical Instruments. H.M.STATIONARY, LONDON. 1920.
- Conrady亚历山大·尤金·康拉迪, Alexander Eugen. applied Optics & Optical design. DOVER PUBLICATION. 1957.
- Kingslake 鲁道夫·京斯莱克, Rudolf. LENS DESIGN FUNDAMENTALS. ACADEMIC PRESS,NEW YORK. 1978. ISBN 012374301X.