File:Kerr photon orbit with zero axial angular momentum.gif
Kerr_photon_orbit_with_zero_axial_angular_momentum.gif (758 × 500像素,文件大小:7.38 MB,MIME类型:image/gif、循环、393帧、17秒)
注意:由于技术限制,高分辨率GIF图像的缩略图无法进行动画处理。
目录
摘要
| 描述Kerr photon orbit with zero axial angular momentum.gif |
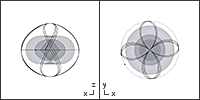
Deutsch: Photonenorbit um ein mit mit dem Spinparameter a=Jc/G/M²=1 rotierendes schwarzes Loch. Der Boyer-Lindquist Radius ist konstant r⊥°=(1+√2)GM/c². Axialer Drehimpuls: Lz=0 (aufgrund des Frame-Dragging-Effekts ist der beobachtete Inklinationswinkel kleiner als 90°; für die Version auf r⊥°=3GM/c² mit scheinbar verschwindendem axialen Drehimpuls, in der dieser den Effekt des Frame-Draggings genau aufhebt geht es hier entlang.
English: Photon-orbit around a rotating black hole with the spin-parameter a=Jc/G/M²=1. The Boyer-Lindquist radius is constant at r⊥°=(1+√2)GM/c². Because of the inertial-frame-dragging the zero axial angular momentum, Lz=0, gives an observed inclination angle of smaller than 90°; for a version where a negative Lz exactly cancels out the equatorial fram-dragging click here. |
| 日期 | |
| 来源 | 自己的作品 Text: de.wikipedia.org/wiki/Kerr-Metrik, other versions: photon orbit @ r=3 |
| 作者 | Yukterez (Simon Tyran, Vienna) |
| 其他版本 |
  |
Display
en
01) Coordinate time 08) Axial radius of gyration 15) Axial angular momentum 22) Framedragging delayed angular velocity 02) Affine parameter 09) Poloidial radius of gyration 16) Polar angular momentum 23) Framedragging local velocity 03) Total time dilation 10) Radial coefficient 17) Radial momentum 24) Framedragging observed velocity 04) Gravitational time dilation 11) E kinetic 18) Cartesian radius 25) Observed particle velocity 05) Boyer Lindquist radius 12) Potential energy component 19) Cartesian X-axis 26) Local escape velocity 06) BL Longitude in radians 13) Total particle energy 20) Cartesian Y-axis 27) Delayed particle velocity 07) BL Latitude in radians 14) Carter Constant 21) Cartesian Z-axis 28) Local particle velocity
de
01) Koordinatenzeit 08) Axialer Gyrationsradius 15) Axialer Drehimpuls 22) Framedrag verzögerte Winkelgeschwindigkeit 02) Affiner Parameter 09) Poloidialer Gyrationsradius 16) Polarer Drehimpuls 23) Framedrag lokale Transversalgeschwindigkeit 03) Insgesamte Zeitdilatation 10) Radialer Vorfaktor 17) Radialer Impuls 24) Framedrag beobachtete Transversalgeschwindigkeit 04) Gravitative Zeitdilatation 11) E kinetisch 18) Kartesischer Radius 25) Beobachtete Totalgeschwindigkeit 05) Boyer Lindquist Radius 12) Potentielle Energie 19) Kartesische X-Achse 26) Lokale Fluchtgeschwindigkeit 06) BL Längengrad in Radianten 13) Totale Energie 20) Kartesische Y-Achse 27) Verzögerte Geschwindigkeit 07) BL Breitengrad in Radianten 14) Carter Konstante 21) Kartesische Z-Achse 28) Lokale Geschwindigkeit relativ zum ZAMO
Bahnneigungswinkel nach Radius
Für ein gegebenes a und r und ausgehend von θ0=π/2 kann der benötigte Bahnneigungswinkel δ0 für die Kreisbahn eines Photons gefunden werden indem[1]

gesetzt und nach δ0 aufgelöst wird. Die realen Lösungen des Polynoms geben eine mögliche Bahn in die positive, und eine in die negative z-Richtung (aufgrund der axialen Symmetrie sind auf einem r jeweils 2 zueinander gespiegelte Orbits möglich). Die Terme der obigen Gleichung sind:




Bewegungsgleichungen
Alle Formeln sind in natürlichen Einheiten:

Koordinatenzeitableitung nach der Eigenzeit (dt/dτ), wobei τ für masselose Testteilchen zum affinen Parameter λ wird:

Radialkoordinatenableitung (dr/dτ):

Radiale Impulskomponentenableitung:

Zusammenhang mit der lokalen Geschwindigkeit:

Breitengradableitung (dθ/dτ):

Drehimpulsableitung auf der θ-Achse (pθ/dτ):

Zusammenhang mit der lokalen Geschwindigkeit:

Längengradableitung (dФ/dτ):

Drehimpulsableitung auf der Ф-Achse (pФ/dτ):

Erhaltungsgröße Carter-Konstante:

Daraus abgeleitete Erhaltungsgröße:

Erhaltungsgröße Gesamtenergie:

Erhaltungsgröße Drehimpuls entlang Ф:

mit dem Radius der Gyration

Frame Dragging Winkelableitung (dФ/dt):

Gravitative Zeitdilatationskomponente (dt/dτ):

Lokale Geschwindigkeit auf der r-Achse:

Lokale Geschwindigkeit auf der θ-Achse:

Lokale Geschwindigkeit auf der Ф-Achse:

Kartesische Koordinaten:

Beobachtete Geschwindigkeit:

Die radiale Fluchtgeschwindigkeit ergibt sich aus dem Verhältnis:

zusammengefasste Terme:

en
For an english version of the equations of motions click here
Referenzen
- ↑ Simon Tyran: Kreisbahnen in der Kerr-Raumzeit
- ↑ Pu, Yun, Younsi & Yoon: General-relativistic radiative transfer in Kerr spacetime, S. 2+
- ↑ Janna Levin & Gabe Perez-Giz: A Periodic Table for Black Hole Orbits, S. 30+
- ↑ Scott A. Hughes: Nearly horizon skimming orbits of Kerr black holes, S. 5+
- ↑ Janna Levin & Gabe Perez-Giz: The Phase Space Portrait, S. 2+
- ↑ Misner, Thorne & Wheeler (MTW): Die Bibel archive copy at the Wayback Machine, S. 897+
- ↑ Simon Tyran: Kerr Orbits / Gravitationslinsen
许可协议
- 您可以自由地:
- 共享 – 复制、发行并传播本作品
- 修改 – 改编作品
- 惟须遵守下列条件:
- 署名 – 您必须对作品进行署名,提供授权条款的链接,并说明是否对原始内容进行了更改。您可以用任何合理的方式来署名,但不得以任何方式表明许可人认可您或您的使用。
- 相同方式共享 – 如果您再混合、转换或者基于本作品进行创作,您必须以与原先许可协议相同或相兼容的许可协议分发您贡献的作品。
File usage in Wikipedia articles
de.wikipedia.org/wiki/Kerr-Metrik
| 註解 InfoField | 該圖片含有註解:在維基媒體共享資源上查看註解 |
outer ergosphere
inner and outer horizon
inner ergosphere and ring singularity
说明
此文件中描述的项目
描繪內容
21 7 2017
image/gif
文件历史
点击某个日期/时间查看对应时刻的文件。
| 日期/时间 | 缩略图 | 大小 | 用户 | 备注 | |
|---|---|---|---|---|---|
| 当前 | 2022年11月5日 (六) 23:58 |  | 758 × 500(7.38 MB) | Yukterez | the Q was missing a ² |
| 2017年7月26日 (三) 13:05 |  | 758 × 500(7.38 MB) | Yukterez | accidentally uploaded the much larger file with the observed, but not truly nonzero angular momentum | |
| 2017年7月26日 (三) 12:58 |  | 758 × 500(17.57 MB) | Yukterez | more spacing for the units | |
| 2017年7月25日 (二) 22:41 |  | 758 × 500(7.38 MB) | Yukterez | the energy in the display accidentaly had units of mc² instead of hf | |
| 2017年7月22日 (六) 08:57 |  | 758 × 500(7.4 MB) | Yukterez | setting significant digits in the numerical display to 6 to better fit them into the frame | |
| 2017年7月21日 (五) 10:57 |  | 758 × 500(8.82 MB) | Yukterez | User created page with UploadWizard |
文件用途
没有页面链接到本图像。
元数据
此文件中包含有扩展的信息。这些信息可能是由数码相机或扫描仪在创建或数字化过程中所添加。
如果此文件的源文件已经被修改,一些信息在修改后的文件中将不能完全反映出来。
| 使用软件 | Adobe Photoshop 21.0 (Windows) |
|---|

