莫爾圓

莫爾圓（Mohr's circle）得名自德國土木工程師克里斯汀·奧圖·莫爾，是一種用二維方式表示柯西应力张量轉換關係的圖。

圖1：三維應力下的莫爾圓

先針對假設為連續的物體進行應力分析，之後特定一點的柯西应力张量分量會和坐標系有關。莫爾圓是用圖形的方法去確認一個旋轉坐標系上的應力分量，也就是在同一點上，但是作用在不同方向平面上的分量。

圓上每一個點的橫坐標$\sigma _{\mathrm {n} }$及縱坐標$\tau _{\mathrm {n} }$都是在這個旋轉坐標系統上某一個方向的正應力及剪應力。換句話說，莫爾圓表示了在所有方向平面上應力狀態的軌跡，而X軸和Y軸為應力元素的主軸。

卡爾·卡爾曼是第一個想到用圖形來表示應力的人，他是在分析水平樑承受彎曲時的縱向應力及垂直應力時所想到的。莫爾的貢獻不止是用莫爾圓表示二維及三維的應力，他也根據莫爾圓發展了結構失效判定的準則。

其他表示應力狀態的方式有拉梅應力橢球及柯西應力二次曲線（Cauchy's stress quadric）。

莫爾圓可以擴展到對稱的 2x2 張量，包括應變及轉動慣量張量。

應力及莫爾圓

圖2：在有受力可變形物體（假設為連續體）中的應力F

考慮一個會變形的物體（假設為連續體），若受到外力（可能是表面力或是物體力），物體的內部就會有力的分布。物體內部的力會依循歐拉運動定律，正如物體受力依循牛頓運動定律一様。物體內部力的強度可以用應力來表示。因為物體假設為連續體，其內部的力也是會均勻分佈在其體積中。

在工程中（例如結構工程、機械工程或土力工程）會透過應力分析來分析一物體中應力的的分佈，例如隧道中岩石的應力，飛機機翼的應力，或是建築物中樑柱的應力等。計算應力分布也就表示要知道物體中每一點的應力。據奧古斯丁·路易·柯西的理論，（假設為連續體的）物體中任何一點的應力（圖2），可以完全由二階(2,0)型的張量中的九個應力元素 $\sigma _{ij}$完全決定，此二階張量稱為柯西应力张量, ${\boldsymbol {\sigma }}$:

${\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]$

圖3：連續體中的一點在平面應力條件下的應力轉換

若確定了一物體在特定坐標系統$(x,y)$下的應力分佈，有可能需要知道特定一點$P$相對另一個有旋轉的坐標系統$(x',y')$下的應力張量，也就是在需要關注的點，在特定角度下的的應力張量。而此坐標系統$(x',y')$和原有的坐標系統$(x,y)$之間有一個角度差（圖3）。例如，一般會需要知道最大的正向應力以及最大的剪應力，也需要知道其對應的方向。因此，需要發展一種張量轉換的方式，可以配合坐標系統的旋轉得到新坐標系統的張量。依照張量的定義，柯西应力张量遵守張量轉換定律。應力的莫爾圓是用圖解方式來說明柯西应力张量轉換定律的方式。

二維張量下的莫爾圓

圖4：連續體中的一點在平面應力條件下的應力分量

在二維下，一點$P$相對于垂直方向的應力張量可以用三個應力向量完全表示。在垂直坐標系統$(x,y)$下，其應力分量為：法向應力$\sigma _{x}$及$\sigma _{y}$，以及剪應力$\tau _{xy}$。由於角動量守恆，柯西應力張量會有對稱性，也就是$\tau _{xy}=\tau _{yx}$，因此柯西應力張量可以寫成：

${\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{x}&\tau _{xy}&0\\\tau _{xy}&\sigma _{y}&0\\0&0&0\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{xy}&\sigma _{y}\\\end{matrix}}\right]$

其目的是在另一個通過$P$點，但存在角度差的坐標系統$(x',y')$下，找到應力分量$\sigma _{\mathrm {n} }$及$\tau _{\mathrm {n} }$（圖4）。坐標系統$(x',y')$和原坐標系統$(x,y)$的角度差即為$\theta$。

莫爾圓的方程

要推導二維平面應力及平面應變的莫爾圓方程，先考慮一個位在位置$P$的二維的無限小方形元素（圖4），和$y$-$z$平面平行。

利用無限小元素上的力平衡，正向應力$\sigma _{\mathrm {n} }$及剪應力$\tau _{\mathrm {n} }$的大小為：

$\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta$

$\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta$

莫爾圓參數式的推導－利用力平衡

利用$\sigma _{\mathrm {n} }$方向（$x'$軸）的力平衡（圖4），而且假設$\sigma _{\mathrm {n} }$ 作用的面積為$dA$，可得： $\ {\begin{aligned}\sum F_{x'}&=\sigma _{\mathrm {n} }dA-\sigma _{x}dA\cos ^{2}\theta -\sigma _{y}dA\sin ^{2}\theta -\tau _{xy}dA\cos \theta \sin \theta -\tau _{xy}dA\sin \theta \cos \theta =0\\\sigma _{\mathrm {n} }&=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +2\tau _{xy}\sin \theta \cos \theta \\\end{aligned}}$ 再考慮以下的關係 $\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad$ 及 $\qquad \sin 2\theta =2\sin \theta \cos \theta$ 可以得到 $\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta$ 再考慮$\tau _{\mathrm {n} }$方向（$y'$軸）的力平衡（圖4），再假設 $\tau _{\mathrm {n} }$作用的面積是$dA$，可得： $\ {\begin{aligned}\sum F_{y'}&=\tau _{\mathrm {n} }dA+\sigma _{x}dA\cos \theta \sin \theta -\sigma _{y}dA\sin \theta \cos \theta -\tau _{xy}dA\cos ^{2}\theta +\tau _{xy}dA\sin ^{2}\theta =0\\\tau _{\mathrm {n} }&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)\\\end{aligned}}$ 再考慮以下的關係 $\cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta \qquad$ 及 $\qquad \sin 2\theta =2\sin \theta \cos \theta$ 可以得到 $\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta$

上述二個方程也可以用柯西應力張量的張量變換定律來求得，這和在$\sigma _{\mathrm {n} }$及$\tau _{\mathrm {n} }$方向用力平衡計算是等效的。

莫爾圓參數式的推導－利用張量變換

應力張量變換定律可以表示為 ${\begin{aligned}{\boldsymbol {\sigma }}'&=\mathbf {A} {\boldsymbol {\sigma }}\mathbf {A} ^{T}\\\left[{\begin{matrix}\sigma _{x'}&\tau _{x'y'}\\\tau _{y'x'}&\sigma _{y'}\\\end{matrix}}\right]&=\left[{\begin{matrix}a_{x}&a_{xy}\\a_{yx}&a_{y}\\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}a_{x}&a_{yx}\\a_{xy}&a_{y}\\\end{matrix}}\right]\\&=\left[{\begin{matrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{matrix}}\right]\end{aligned}}$ 將等號右側展開，再配合$\sigma _{x'}=\sigma _{\mathrm {n} }$及$\tau _{x'y'}=\tau _{\mathrm {n} }$，可得： $\sigma _{\mathrm {n} }=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta +2\tau _{xy}\sin \theta \cos \theta$ 再加上以下的條件 $\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad$ 及$\qquad \sin 2\theta =2\sin \theta \cos \theta$ 可得 $\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta$ $\tau _{\mathrm {n} }=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)$ 再加上以下的條件 $\cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta \qquad$ 及$\qquad \sin 2\theta =2\sin \theta \cos \theta$ 可得 $\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta$ 此時不需要計算$\sigma _{x'}$垂直的應力成份$\sigma _{y'}$，因為在推導莫爾圓時還不需要此成份

這二個方程是莫爾圓的參數式。在方程中，$2\theta$為參數，而$\sigma _{\mathrm {n} }$和$\tau _{\mathrm {n} }$為坐標，因此表示若選擇適當的坐標系統，使$\sigma _{\mathrm {n} }$為橫軸，$\tau _{\mathrm {n} }$縱軸，給定參數$\theta$，會給定在莫爾圓上的一點。

若從參數式中消去參數$2\theta$，可以得到非參數式的莫爾圓方程。可以用重組$\sigma _{\mathrm {n} }$及$\tau _{\mathrm {n} }$的方程來達到。先將第一式等號右側的第一項移到等號左邊，二式平方後相加，可得

${\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\\(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}&=R^{2}\end{aligned}}$

其中

$R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})$

這就是圓（莫爾圓）的方程

$(x-a)^{2}+(y-b)^{2}=r^{2}$

在$(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$坐標系統中，其半徑$r=R$，圓心在坐標$(a,b)=(\sigma _{\mathrm {avg} },0)$處。

符號體系

在使用莫爾圓時，需考慮兩組分別的符號體系，一個是針對實體空間下應力分量的符號體系，另一個是針對「莫爾圓空間」下應力分量的符號體系。此外，工程力學（結構工程及機械工程）文獻用的體系和地質力學用的符號體系不同。沒有所有系統都適用的標準符號體系，是否要使用特定的符號體系取決於計算及詮釋特定問題的方便程度。

上述圖4的莫爾圓推導都是使用工程力學的符號體系，以下也會繼續使用工程力學的符號體系。

實體空間符號體系

為了描述柯西應力張量的方便（圖3及圖4），應力分量的第一個下標表示應力分量作用的面，第二個下標表示應力分量的方向。因此$\tau _{xy}$是作用在以$x$軸正向為其法向量的平面上，而方向是往$y$軸的正方向。

在實體空間符號體系，正的正向應力是由作用平面往外（張力），負的正向應力是由作用平面往內（壓縮力）（圖5）。

在實體空間符號體系中，正剪應力在法向量為正的材料元素平面上，其作用方向會往軸的正方向，同樣的，正剪力在法向量為負的材料元素平面上，其作用方向會往軸的負方向。例如作用在正向平面的剪應力$\tau _{xy}$和$\tau _{yx}$為正，因為這二個剪應力的作用方向往$y$軸及$x$軸的正方向（圖3）。而相對應的作用在負向平面的剪應力$\tau _{xy}$和$\tau _{yx}$，其作用方向往$y$軸及$x$軸的負方向，因此這二個剪應力也為正。

莫爾圓空間符號體系

圖5 繪制莫爾圓時，工程力學符號體系下的應力。此條目會依照圖中的符號體系 # 3

在莫爾圓空間符號體系中，應力的符號體系和實體空間符號體系中的相同：正的正向應力是由作用平面往外（張力），負的正向應力是由作用平面往內（壓縮力）

不過剪應力的符號體系和實體空間符號體系中的不同。在莫爾圓空間符號體系中，正的剪應力會使材料往逆時針方向旋轉，而負的剪應力會使材料往順時針方向旋轉。因此在莫爾圓空間中，剪應力分量$\tau _{xy}$為正，而$\tau _{yx}$為負。這和實體空間符號體系中$\tau _{xy}$和$\tau _{yx}$符號相同的情形不同。

在繪製莫爾圓時，有二個作法可以繪製在數學上正確的莫爾圓：

1. 將正的剪應力畫在上方（圖5，符號體系#1）
2. 將正的剪應力畫在下方，也就是$\tau _{\mathrm {n} }$軸倒置（圖5，符號體系#2）

將正的剪應力畫在上方會讓莫爾圓上的$2\theta$角為正值時，旋轉方向是順時針旋轉，這和實體空間符號體系中的相反。因此有些作者會選擇讓正的剪應力畫在下方，這會讓莫爾圓上的$2\theta$角為正值時，旋轉方向是逆時針旋轉，類似實體空間符號體系的情形。

為了克服剪應力軸往下才是正向的問題，有另外一種「替代的」符號體系，其中正的剪應力假設為將材料將順時針方向旋轉，而負的剪應力假設為將材料將逆時針方向旋轉（圖5，符號體系#3）。在「替代」體系下，正的剪應力軸往上，而且在莫爾圓上$2\theta$為正值時，旋轉方向為逆時針。此符號體系產生的莫爾圓和圖5，符號體系#2中的相同，因為正的剪應力$\tau _{\mathrm {n} }$也是會逆時針旋轉的剪應力，也畫在下方。而負的剪應力$\tau _{\mathrm {n} }$也是會順時針旋轉的剪應力，也畫在上方。

此條目在實體空間符號體系中，會依照工程力學的符號體系，而在莫爾圓空間中，會使用「替代的」符號體系（圖5，符號體系#3）。

繪製莫爾圓

圖6：在平面應力及平面應變的條件下繪製莫爾圓（二倍角的作法）
在應力分析後，可以找到材料中一點$P$上的應力分量$\sigma _{x}$、$\sigma _{y}$及$\tau _{xy}$。應力分量作用在二個互相垂直的$A$平面及$B$平面，兩者都通過$P$點。莫爾圓上$A$點和 $B$點的坐標是在$A$平面及$B$平面上的應力分量。因此可以用莫爾圓找到應力分量$\sigma _{\mathrm {n} }$及$\tau _{\mathrm {n} }$，也就是在同一點上，但作用在其他平面$D$上的應力分量。${\overline {OB}}$線和${\overline {OD}}$線之間的夾角是通過$P$點的平面$B$和平面$D$的法向量的夾角

假設已知待研究物體上的點$P$的應力分量$\sigma _{x}$、$\sigma _{y}$及$\tau _{xy}$，如圖4所示。以下方法可以繪製點$P$的莫爾圓，以表示其應力狀態。

1. 繪制笛卡爾坐標系統$(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$，橫軸為$\sigma _{\mathrm {n} }$，縱軸為$\tau _{\mathrm {n} }$。
2. 在$(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$空間中，畫出二點$A(\sigma _{y},\tau _{xy})$及$B(\sigma _{x},-\tau _{xy})$，分別是作用在二垂直平面$A$平面和 $B$平面上的應力分量（圖4及圖6），需依照選擇的符號體系。
3. 用線段${\overline {AB}}$連接$A$點和$B$點，此即為圓的直徑。
4. 繪製莫爾圓，其圓心$O$是線段${\overline {AB}}$的中點，也就是此線和$\sigma _{\mathrm {n} }$軸的交點。

找主要正向應力

主要應力的大小是點$C$和點$E$（圖6中圓和 $\sigma _{\mathrm {n} }$軸的交點）中的橫坐標。最大正向應力$\sigma _{1}$的大小恆為這二個橫坐標中最大的那一個，而$\sigma _{2}$最小正向應力的大小恆為這二個橫坐標中最小的那一個。這二個點的縱坐標為0，對應在主要平面上的剪應力為零，主要應力的大小也可以表示為

$\sigma _{1}=\sigma _{\max }=\sigma _{\text{avg}}+R$

$\sigma _{2}=\sigma _{\min }=\sigma _{\text{avg}}-R$

其中平均正向應力$\sigma _{\text{avg}}$的大小是圓心$O$的橫坐標，為

$\sigma _{\text{avg}}={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})$

其半徑的長度$R$為

$R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}$

找最大和最小剪應力

最大剪應力和最小剪應力對應圓上最大及最小的縱坐標。這二個點是圓和通過圓心$O$的垂直線的交點。因此，最大和最小剪應力的大小為圓的半徑$R$

$\tau _{\max ,\min }=\pm R$

找任意平面的應力分量

如前面所述，在二維應力分析後，可以知道在材料某一點$P$上的應力分量$\sigma _{x}$、$\sigma _{y}$及 $\tau _{xy}$。這些應力分量作用在通過$P$點的二垂直平面 $A$ 及 $B$，如圖5及圖6所述。莫爾圓也可以計算在莫爾圓上$D$的應力分量$\sigma _{\mathrm {n} }$及$\tau _{\mathrm {n} }$，事實是作用在$D$平面上，此平面也通過$P$點，和$B$平面有夾角$\theta$，計算應力分量有二種方式：倍角法以及平面原點法（origin of planes）

倍角法

如圖6所示，若平面$D$是平面$B$再逆時針旋轉角度$\theta$後的平面，要找到在平面$D$上的應力分量$(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$，可以在莫爾圓上從已知應力點 $B(\sigma _{x},-\tau _{xy})$同樣以逆時針旋轉，但旋轉角度 $2\theta$，旋轉到點$D(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$，也就是讓${\overline {OB}}$線和${\overline {OD}}$線之間的夾角是$2\theta$。

倍角法的作法源自於通過$P$點的二實際平面之間的夾角$\theta$（圖4），是其對應應力點 $(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$在莫爾圓上和圓心連線形成夾角的一半。

倍角關係是因為莫爾圓的參數式是$2\theta$的函數。也可以從在材料點 $P$上的平面$A$和$B$夾角是90度，而在莫爾圓上其應力點夾角為180度看出（90度的兩倍）。

極點法（或平面原點法）

圖7：平面應力及應變的莫爾圓（極點法）。從極點畫的任何直線都會和莫爾圓相交，交點表示在和直線相同角度平面上的應力狀態

第二種方式和要找到莫爾圓上的一個點，稱為極點（pole）或是平面原點（origin of planes）。從極點畫的任何直線都會和莫爾圓相交，交點表示在和直線相同角度的平面上的應力狀態。因此若知道任何特定平面上的應力分量$\sigma$及$\tau$，可以畫一條線通過莫爾圓上的 $\sigma _{\mathrm {n} }$和$\tau _{\mathrm {n} }$，且和平面平行，找到莫爾圓上這些線的交點，即為極點。例如，假設有應力狀態如圓7所示，其分量是$\sigma _{x},\!$, $\sigma _{y},\!$及$\tau _{xy},\!$。首先先從$B$點畫一條線，平行$\sigma _{x}$的作用平面，或是從$A$點畫一條線，平行$\sigma _{y}$的作用平面，任一條線都會和莫爾圓交會，交會的點即為極點。在找到極點後，若要找到和垂直有$\theta$夾角的平面上的應力，可以從極點畫一條平行該平面的線（見圖7）。可以根據直線和莫爾圓的交點找到平面上的正向應力以及剪應力。

找主要平面的方向

最大主要應力及最小主要應力所在的平面方向也稱為主要平面（principal planes），可以用莫爾圓中 的∠BOC及∠BOE判斷，然後將二個角度都取一半。因此${\overline {OB}}$和${\overline {OC}}$之間的夾角是角∠BOC，是$\theta _{p}$（主要平面和平面$B$夾角）角度的二倍。

而$\theta _{p1}$和$\theta _{p2}$也可以用以下的方程取得

$\tan 2\theta _{\mathrm {p} }={\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}$

此方程的解會是二個角度，彼此相差$90^{\circ }$。可以直接用圓的幾何求解此方程，或是用圓的參數式，並且讓$\tau _{\mathrm {n} }$等於零（主要平面上的剪應力為0）。

一般三維應力下的莫爾圓

圖10 三維應力下的莫爾圖

若要繪製三維應力下的莫爾圖，需要先量測其主應力的大小$\left(\sigma _{1},\sigma _{2},\sigma _{3}\right)$以及方向$\left(n_{1},n_{2},n_{3}\right)$。

考慮以主應力軸為坐標系統，而不是用$x_{1}$, $x_{2}$, $x_{3}$坐標系統，並且假設$\sigma _{1}>\sigma _{2}>\sigma _{3}$，則在一法向量為 $\mathbf {n}$的平面，其應力向量$\mathbf {T} ^{(\mathbf {n} )}$的應力分量及剪力分量會滿足下式

${\begin{aligned}\left(T^{(n)}\right)^{2}&=\sigma _{ij}\sigma _{ik}n_{j}n_{k}\\\sigma _{\mathrm {n} }^{2}+\tau _{\mathrm {n} }^{2}&=\sigma _{1}^{2}n_{1}^{2}+\sigma _{2}^{2}n_{2}^{2}+\sigma _{3}^{2}n_{3}^{2}\end{aligned}}$

$\sigma _{\mathrm {n} }=\sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}.$

由於$n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1$，可以用高斯消去法求解$n_{1}^{2}$, $n_{2}^{2}$, $n_{3}^{2}$：

${\begin{aligned}n_{1}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {n} }-\sigma _{3})}{(\sigma _{1}-\sigma _{2})(\sigma _{1}-\sigma _{3})}}\geq 0\\n_{2}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})}{(\sigma _{2}-\sigma _{3})(\sigma _{2}-\sigma _{1})}}\geq 0\\n_{3}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})}{(\sigma _{3}-\sigma _{1})(\sigma _{3}-\sigma _{2})}}\geq 0.\end{aligned}}$

因為$\sigma _{1}>\sigma _{2}>\sigma _{3}$及$(n_{i})^{2}$都不是負值，因此其分子滿足

$\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {n} }-\sigma _{3})\geq 0$ 因為其分母$\sigma _{1}-\sigma _{2}>0$而且$\sigma _{1}-\sigma _{3}>0$

$\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})\leq 0$ 因為其分母$\sigma _{2}-\sigma _{3}>0$而且$\sigma _{2}-\sigma _{1}<0$

$\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})\geq 0$ 因為其分母$\sigma _{3}-\sigma _{1}<0$而且$\sigma _{3}-\sigma _{2}<0.$

方程式可以寫成

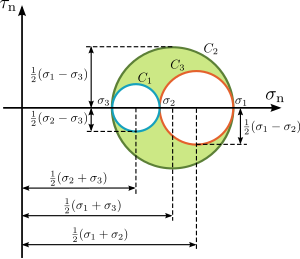
${\begin{aligned}\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3})\right]^{2}\leq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\end{aligned}}$

是三個應力莫爾圓$C_{1}$, $C_{2}$和$C_{3}$的方程，其半徑分別是$R_{1}={\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})$, $R_{2}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})$及$R_{3}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})$，而其圓心分別在$\left[{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3}),0\right]$, $\left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]$, $\left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2}),0\right]$。

有了上述三個應力莫爾圓的方程，所有可能的應力點$(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$都會在三個應力莫爾圓之間的陰影區域（見圖10）。應力點$(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })$ 可能滿足圓$C_{1}$的方程，或是在圓$C_{1}$的外面，可能滿足圓$C_{2}$的方程，或是在圓$C_{2}$的裡面，可能滿足圓$C_{3}$的方程，或是在圓$C_{3}$的外面。

相關條目

• 臨界面分析

參考資料

• Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf. Mechanics of Materials. McGraw-Hill Professional. 1992. ISBN 0-07-112939-1. 
• Brady, B.H.G.; E.T. Brown. Rock Mechanics For Underground Mining Third. Kluwer Academic Publisher. 1993: 17–29 [2018-02-05]. ISBN 0-412-47550-2. （原始内容存档于2020-08-07）. 
• Davis, R. O.; Selvadurai. A. P. S. Elasticity and geomechanics. Cambridge University Press. 1996: 16–26 [2018-02-05]. ISBN 0-521-49827-9. （原始内容存档于2020-08-07）. 
• Holtz, Robert D.; Kovacs, William D. An introduction to geotechnical engineering. Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. 1981 [2018-02-05]. ISBN 0-13-484394-0. （原始内容存档于2019-06-08）. 
• Jaeger, John Conrad; Cook, N.G.W; Zimmerman, R.W. Fundamentals of rock mechanics Fourth. Wiley-Blackwell. 2007: 9–41 [2018-02-05]. ISBN 0-632-05759-9. （原始内容存档于2019-06-02）. 
• Jumikis, Alfreds R. Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering. Van Nostrand Reinhold Co. 1969 [2018-02-05]. ISBN 0-442-04199-3. （原始内容存档于2019-06-08）. 
• Parry, Richard Hawley Grey. Mohr circles, stress paths and geotechnics 2. Taylor & Francis. 2004: 1–30 [2018-02-05]. ISBN 0-415-27297-1. （原始内容存档于2020-08-07）. 
• Timoshenko, Stephen P.; James Norman Goodier. Theory of Elasticity Third. McGraw-Hill International Editions. 1970. ISBN 0-07-085805-5. 
• Timoshenko, Stephen P. History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures. Dover Books on Physics. Dover Publications. 1983. ISBN 0-486-61187-6. 

外部連結

• Mohr's Circle and more circles by Rebecca Brannon （页面存档备份，存于互联网档案馆）
• DoITPoMS Teaching and Learning Package- "Stress Analysis and Mohr's Circle" （页面存档备份，存于互联网档案馆）