龍格現象
在數值分析領域中,龍格現象是在一組等間插值點上使用具有高次多項式的多項式插值時出現的區間邊緣處的振盪問題。 它是由卡爾·龍格(Carl Runge)在探索使用多項式插值逼近某些函數時的錯誤行為時發現的。[1]這一發現非常重要,因為它表明使用高次多項式插值並不總能提高準確性。 該現象與傅里葉級數近似中的吉布斯現象相似。
介紹 編輯
魏爾斯特拉斯逼近定理表明,對於定義在區間 上的每個連續函數 ,存在一組多項式函數 ,當n趨向於無窮大時,近似於 上具有一致收斂的 ,也就是說,
考慮使用通過那些點的 次多項式 來插值計算通過函數 的 個等間隔點的情況。自然地,可以從魏爾斯特拉斯的定理中期望使用更多的點將導致 的更準確的重構。然而,這組特定的多項式函數 並不能保證具有一致收斂的性質;該定理僅指出存在一組多項式函數,而沒有提供找到一個的一般方法。
隨着 的增加,以這種方式產生的 實際上可能偏離 ;這通常發生在靠近插值點的端點。這種現象以龍格命名。[2]
問題 編輯
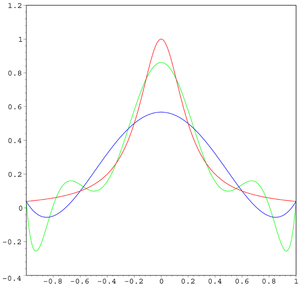
考慮以下龍格函數:
龍格發現如果使用 階多項式 在 −1 與 1 之間按照
這樣的等距點xi 進行插值,那麼在接近端點 −1 與 1 的地方插值結果就會出現震盪。
可以證明,在多項式的階數增高時插值誤差甚至會趨向無限大:
解決龍格現象的辦法 編輯
使用切比雪夫節點代替等距點可以減小震盪,在這種情況下,隨着多項式階次的增加最大誤差逐漸減小。這個現象表明高階多項式通常不適合用於插值。使用分段多項式樣條可以避免這個問題。如果要減小插值誤差,那麼可以增加構成樣條的多項式的數目,而不必是增加多項式的階次。
參考文獻 編輯
- ^ Runge, Carl, Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten, Zeitschrift für Mathematik und Physik, 1901, 46: 224–243. available at www.archive.org
- ^ Epperson, James. On the Runge example. Amer. Math. Monthly. 1987, 94: 329–341 [2018-04-27]. doi:10.2307/2323093. (原始內容存檔於2020-09-25).
參見 編輯
- 與正弦基函數吉布斯現象的比較
- 《數值分析》,清華大學出版社,李慶揚等編,書號ISBN 978-7-302-18565-9