馬丟函數(法語:Équation de Mathieu)是1868年法國數學家以米里迂·拉·馬丟因研究數學物理所推得的特殊函數,下列馬丟方程的解析解:
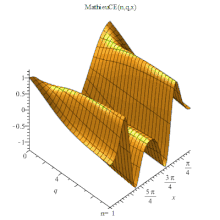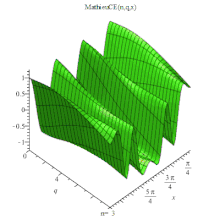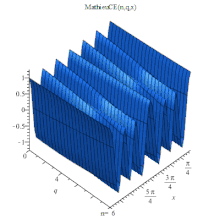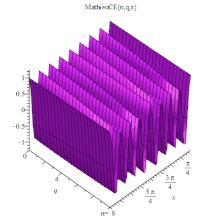 MathieuCE 3D
MathieuCE 3D
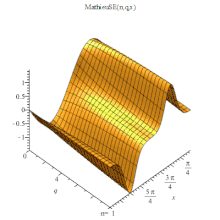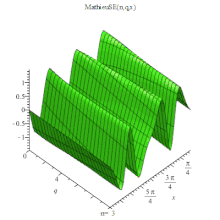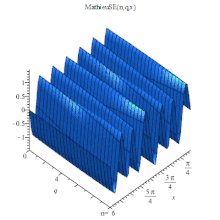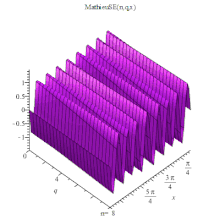 MathieuSE 3D
MathieuSE 3D
![{\displaystyle {\frac {d^{2}y}{dx^{2}}}+[a-2q\cos(2x)]y=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04350d53213611e9b1c2cd83f8541ee52b225496)
馬丟方程有兩個線性無關的解:
- 奇數解
MathieuCE(n, q, x),或記為 ,
,
- 偶數解
MathieuSE(n, q, x).或記為 稱為基本解[1]
稱為基本解[1]
馬丟函數 MathieuC(a,q,z) 或 MathieuS(a,q,z) 只有一個是周期為 或 的周期解,另一個不是。
馬丟函數 MathieuC(a,q,z) 和 MathieuS(a,q,z) 兩者都有是周期為 (n≥2)的周期函數。
[1]
-
-
-
Mathieu Eigen value a(n,q)
Mathieu eigenvalue b(n,q)
馬丟方程的特徵方程是[1]
對於給定的v,q, 上列特徵方程給出無窮多個a、b解稱為特徵值。
馬丟函數體特徵值可展開成級數:[2]
馬丟函數ce,se的級數展開[3]
馬丟函數的傅立葉展開:[3]
-
-
-
-
其中係數A,B滿足下列遞歸關係:[3]
馬丟方程的基本解 滿足下列關係:[3]:
- =
郎斯基行列式:




-
-
-
-
-
-

Mathieu Floquet
馬丟函數中,如果 是一個周期為 的解,並滿足下列條件
,其中 與x 無關,則此解稱為夫洛開解。
- 級數展開
- ^ 1.0 1.1 1.2 王竹溪 郭敦仁 603 引用錯誤:帶有name屬性「W」的
<ref>標籤用不同內容定義了多次
- ^ Frank p659
- ^ 3.0 3.1 3.2 3.3 Frank p660 引用錯誤:帶有name屬性「F」的
<ref>標籤用不同內容定義了多次
- 王竹溪 郭敦仁 《特殊函數概論》 第十二章 馬丟函數 北京大學出版社 2000
- Frank J Oliver NIST Handbook of Mathematical Functions,Cambridge University PRESS, 2010


![{\displaystyle {\frac {d^{2}y}{dx^{2}}}+[a-2q\cos(2x)]y=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04350d53213611e9b1c2cd83f8541ee52b225496)


