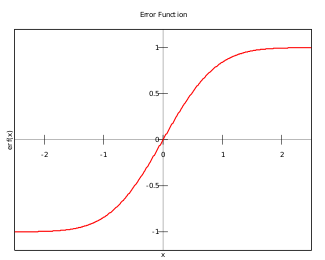
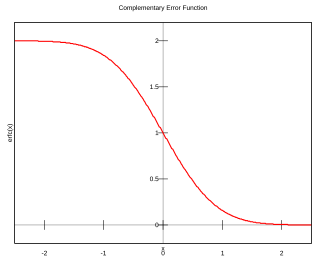
互补误差函数 ,记为 erfc,在误差函数的基础上定义:
erfc
(
x
)
=
1
−
erf
(
x
)
=
2
π
∫
x
∞
e
−
t
2
d
t
.
{\displaystyle {\mbox{erfc}}(x)=1-{\mbox{erf}}(x)={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\,.}
虚误差函数 ,记为 erfi ,定义为:
erfi
(
z
)
=
−
i
erf
(
i
z
)
.
{\displaystyle \operatorname {erfi} (z)=-i\,\,\operatorname {erf} (i\,z).}
複誤差函數 ,记为w (z ),也在误差函数的基础上定义:
w
(
z
)
=
e
−
z
2
erfc
(
−
i
z
)
.
{\displaystyle w(z)=e^{-z^{2}}{\textrm {erfc}}(-iz).}
误差函数来自测度论 ,后来与测量 误差无关的其他领域也用到这一函数,但仍然使用误差函数这一名字。
误差函数与标准正态分布 的积分累积分布函数
Φ
{\displaystyle \Phi }
[ 2]
Φ
(
x
)
=
1
2
+
1
2
erf
(
x
2
)
.
{\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right).}
误差函数是奇函数 :
erf
(
−
z
)
=
−
erf
(
z
)
{\displaystyle \operatorname {erf} (-z)=-\operatorname {erf} (z)}
对于任何 复数 z :
erf
(
z
¯
)
=
erf
(
z
)
¯
{\displaystyle \operatorname {erf} ({\overline {z}})={\overline {\operatorname {erf} (z)}}}
其中
z
¯
{\displaystyle {\overline {z}}}
z 的 复共轭 。
复平面上,函数 ƒ = exp(−z 2 ) 和 ƒ = erf(z ) 如图所示。粗绿线表示 Im(ƒ ) = 0,粗红线表示 Im(ƒ ) < 0, 粗蓝线为 Im(ƒ ) > 0。细绿线表示 Im(ƒ ) = constant,细红线表示 Re(ƒ ) = constant<0,细蓝线表示 Re(ƒ ) = constant>0。
在实轴上, z → ∞时,erf(z ) 趋于1,z → −∞时,erf(z ) 趋于−1 。在虚轴上, erf(z ) 趋于 ±i∞。
误差函数是整函数 ,没有奇点(无穷远处除外),泰勒展开收敛。
误差函数泰勒级数:
erf
(
z
)
=
2
π
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
n
!
(
2
n
+
1
)
=
2
π
(
z
−
z
3
3
+
z
5
10
−
z
7
42
+
z
9
216
−
⋯
)
{\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\ \cdots \right)}
对每个复数 z 均成立。
上式可以用迭代形式表示:
erf
(
z
)
=
2
π
∑
n
=
0
∞
(
z
∏
k
=
1
n
−
(
2
k
−
1
)
z
2
k
(
2
k
+
1
)
)
=
2
π
∑
n
=
0
∞
z
2
n
+
1
∏
k
=
1
n
−
z
2
k
{\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}}
误差函数的导数 :
d
d
z
e
r
f
(
z
)
=
2
π
e
−
z
2
.
{\displaystyle {\frac {\rm {d}}{{\rm {d}}z}}\,\mathrm {erf} (z)={\frac {2}{\sqrt {\pi }}}\,e^{-z^{2}}.}
误差函数的 不定积分 为:
z
erf
(
z
)
+
e
−
z
2
π
{\displaystyle z\,\operatorname {erf} (z)+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}}
逆誤差函數 逆误差函数 可由 麦克劳林级数 表示:
erf
−
1
(
z
)
=
∑
k
=
0
∞
c
k
2
k
+
1
(
π
2
z
)
2
k
+
1
,
{\displaystyle \operatorname {erf} ^{-1}(z)=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},\,\!}
其中, c 0 = 1 ,
c
k
=
∑
m
=
0
k
−
1
c
m
c
k
−
1
−
m
(
m
+
1
)
(
2
m
+
1
)
=
{
1
,
1
,
7
6
,
127
90
,
4369
2520
,
…
}
.
{\displaystyle c_{k}=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},\ldots \right\}.}
即:
erf
−
1
(
z
)
=
1
2
π
(
z
+
π
12
z
3
+
7
π
2
480
z
5
+
127
π
3
40320
z
7
+
4369
π
4
5806080
z
9
+
34807
π
5
182476800
z
11
+
⋯
)
.
{\displaystyle \operatorname {erf} ^{-1}(z)={\tfrac {1}{2}}{\sqrt {\pi }}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).\ }
逆互补误差函数 定义为:
erfc
−
1
(
1
−
z
)
=
erf
−
1
(
z
)
.
{\displaystyle \operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}(z).}
互补误差函数的渐近展开 ,
e
r
f
c
(
x
)
=
e
−
x
2
x
π
[
1
+
∑
n
=
1
∞
(
−
1
)
n
1
⋅
3
⋅
5
⋯
(
2
n
−
1
)
(
2
x
2
)
n
]
=
e
−
x
2
x
π
∑
n
=
0
∞
(
−
1
)
n
(
2
n
−
1
)
!
!
(
2
x
2
)
n
,
{\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}},\,}
其中 (2n – 1)!! 为 双阶乘 ,x 为实数,该级数对有限 x 发散。对于
N
∈
N
{\displaystyle N\in \mathbb {N} }
e
r
f
c
(
x
)
=
e
−
x
2
x
π
∑
n
=
0
N
−
1
(
−
1
)
n
(
2
n
−
1
)
!
!
(
2
x
2
)
n
+
R
N
(
x
)
{\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}}+R_{N}(x)\,}
其中余项用以 大O符号 表示为
R
N
(
x
)
=
O
(
x
−
2
N
+
1
e
−
x
2
)
{\displaystyle R_{N}(x)=O(x^{-2N+1}e^{-x^{2}})}
x
→
∞
{\displaystyle x\to \infty }
余项的精确形式为:
R
N
(
x
)
:=
(
−
1
)
N
π
2
−
2
N
+
1
(
2
N
)
!
N
!
∫
x
∞
t
−
2
N
e
−
t
2
d
t
,
{\displaystyle R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{-2N+1}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t,}
对于比较大的 x, 只需渐近展开中开始的几项就可以得到 erfc(x )很好的近似值。[ 註 3]
互补误差函数的连分式展开形式:[ 3]
e
r
f
c
(
z
)
=
z
π
e
−
z
2
a
1
z
2
+
a
2
1
+
a
3
z
2
+
a
4
1
+
⋯
a
1
=
1
,
a
m
=
m
−
1
2
,
m
≥
2.
{\displaystyle \mathrm {erfc} (z)={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {a_{1}}{z^{2}+{\cfrac {a_{2}}{1+{\cfrac {a_{3}}{z^{2}+{\cfrac {a_{4}}{1+\dotsb }}}}}}}}\qquad a_{1}=1,\quad a_{m}={\frac {m-1}{2}},\quad m\geq 2.}
erf
(
x
)
≈
1
−
1
(
1
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
a
4
x
4
)
4
{\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4})^{4}}}}
−4 )其中, a 1 = 0.278393, a 2 = 0.230389, a 3 = 0.000972, a 4 = 0.078108
erf
(
x
)
≈
1
−
(
a
1
t
+
a
2
t
2
+
a
3
t
3
)
e
−
x
2
,
t
=
1
1
+
p
x
{\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+a_{3}t^{3})e^{-x^{2}},\quad t={\frac {1}{1+px}}}
−5 )其中, p = 0.47047, a 1 = 0.3480242, a 2 = −0.0958798, a 3 = 0.7478556
erf
(
x
)
≈
1
−
1
(
1
+
a
1
x
+
a
2
x
2
+
⋯
+
a
6
x
6
)
16
{\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+\cdots +a_{6}x^{6})^{16}}}}
−7 )其中, a 1 = 0.0705230784, a 2 = 0.0422820123, a 3 = 0.0092705272, a 4 = 0.0001520143, a 5 = 0.0002765672, a 6 = 0.0000430638
erf
(
x
)
≈
1
−
(
a
1
t
+
a
2
t
2
+
⋯
+
a
5
t
5
)
e
−
x
2
,
t
=
1
1
+
p
x
{\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+\cdots +a_{5}t^{5})e^{-x^{2}},\quad t={\frac {1}{1+px}}}
−7 )其中, p = 0.3275911, a 1 = 0.254829592, a 2 = −0.284496736, a 3 = 1.421413741, a 4 = −1.453152027, a 5 = 1.061405429
以上所有近似式适用范围是: x ≥ 0. 对于负的 x , 误差函数是奇函数这一性质得到误差函数的值, erf(x ) = −erf(−x ).
另有近似式:
erf
(
x
)
≈
sgn
(
x
)
1
−
exp
(
−
x
2
4
/
π
+
a
x
2
1
+
a
x
2
)
{\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x){\sqrt {1-\exp \left(-x^{2}{\frac {4/\pi +ax^{2}}{1+ax^{2}}}\right)}}}
其中,
a
=
8
(
π
−
3
)
3
π
(
4
−
π
)
≈
0.140012.
{\displaystyle a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.}
该近似式在0或无穷的邻域非常准确,x 整个定义域上,近似式最大误差小于0.00035,取 a ≈ 0.147 ,最大误差可减小到0.00012。[ 4]
逆误差函数近似式:
erf
−
1
(
x
)
≈
sgn
(
x
)
(
2
π
a
+
ln
(
1
−
x
2
)
2
)
2
−
ln
(
1
−
x
2
)
a
−
(
2
π
a
+
ln
(
1
−
x
2
)
2
)
.
{\displaystyle \operatorname {erf} ^{-1}(x)\approx \operatorname {sgn}(x){\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)^{2}-{\frac {\ln(1-x^{2})}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)}}.}
误差函数本质上与标准正态累积分布函数
Φ
{\displaystyle \Phi }
Φ
(
x
)
=
1
2
π
∫
−
∞
x
e
−
t
2
2
d
t
=
1
2
[
1
+
erf
(
x
2
)
]
=
1
2
erfc
(
−
x
2
)
{\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]={\frac {1}{2}}\,\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)}
可整理为如下形式:
e
r
f
(
x
)
=
2
Φ
(
x
2
)
−
1
e
r
f
c
(
x
)
=
2
Φ
(
−
x
2
)
=
2
(
1
−
Φ
(
x
2
)
)
.
{\displaystyle {\begin{aligned}\mathrm {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\\mathrm {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}
Φ
{\displaystyle \Phi }
分位函数 ,即概率单位
probit
(
p
)
=
Φ
−
1
(
p
)
=
2
erf
−
1
(
2
p
−
1
)
=
−
2
erfc
−
1
(
2
p
)
.
{\displaystyle \operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\,\operatorname {erfc} ^{-1}(2p).}
误差函数为标准正态分布的尾概率Q函数
Q
(
x
)
=
1
2
−
1
2
erf
(
x
2
)
=
1
2
erfc
(
x
2
)
.
{\displaystyle Q(x)={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right).}
误差函数是米塔-列夫勒函数 的特例,可以表示为合流超几何函数 ,
e
r
f
(
x
)
=
2
x
π
1
F
1
(
1
2
,
3
2
,
−
x
2
)
.
{\displaystyle \mathrm {erf} (x)={\frac {2x}{\sqrt {\pi }}}\,_{1}F_{1}\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).}
误差函数用正则Γ函数 P和 不完全Γ函数 表示为
erf
(
x
)
=
sgn
(
x
)
P
(
1
2
,
x
2
)
=
sgn
(
x
)
π
γ
(
1
2
,
x
2
)
.
{\displaystyle \operatorname {erf} (x)=\operatorname {sgn} (x)P\left({\tfrac {1}{2}},x^{2}\right)={\operatorname {sgn} (x) \over {\sqrt {\pi }}}\gamma \left({\tfrac {1}{2}},x^{2}\right).}
sgn
(
x
)
{\displaystyle \scriptstyle \operatorname {sgn} (x)\ }
符号函数 .
广义误差函数图像 E n (x ):E 1 (x ) = (1 − e −x )/
π
{\displaystyle \scriptstyle {\sqrt {\pi }}}
E 2 (x ) = erf(x )E 3 (x )E 4 (x )E 5 (x ). 广义误差函数为:
E
n
(
x
)
=
n
!
π
∫
0
x
e
−
t
n
d
t
=
n
!
π
∑
p
=
0
∞
(
−
1
)
p
x
n
p
+
1
(
n
p
+
1
)
p
!
.
{\displaystyle E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,\mathrm {d} t={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}\,.}
其中,E 0 (x )为通过原点的直线,
E
0
(
x
)
=
x
e
π
{\displaystyle \scriptstyle E_{0}(x)={\frac {x}{e{\sqrt {\pi }}}}}
E 2 (x ) 即为误差函数 erf(x )。
x > 0时,广义误差函数可以用Γ函数和 不完全Γ函数表示,
E
n
(
x
)
=
Γ
(
n
)
(
Γ
(
1
n
)
−
Γ
(
1
n
,
x
n
)
)
π
,
x
>
0.
{\displaystyle E_{n}(x)={\frac {\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right)}{\sqrt {\pi }}},\quad \quad x>0.\ }
因此,误差函数可以用不完全Γ函数表示为:
erf
(
x
)
=
1
−
Γ
(
1
2
,
x
2
)
π
.
{\displaystyle \operatorname {erf} (x)=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{\sqrt {\pi }}}.\ }
互补误差函数的迭代积分定义为:
i
n
erfc
(
z
)
=
∫
z
∞
i
n
−
1
erfc
(
ζ
)
d
ζ
.
{\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\int _{z}^{\infty }\mathrm {i} ^{n-1}\operatorname {erfc} \,(\zeta )\;\mathrm {d} \zeta .\,}
可以展开成幂级数:
i
n
erfc
(
z
)
=
∑
j
=
0
∞
(
−
z
)
j
2
n
−
j
j
!
Γ
(
1
+
n
−
j
2
)
,
{\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\Gamma \left(1+{\frac {n-j}{2}}\right)}}\,,}
满足如下对称性质:
i
2
m
erfc
(
−
z
)
=
−
i
2
m
erfc
(
z
)
+
∑
q
=
0
m
z
2
q
2
2
(
m
−
q
)
−
1
(
2
q
)
!
(
m
−
q
)
!
{\displaystyle \mathrm {i} ^{2m}\operatorname {erfc} (-z)=-\mathrm {i} ^{2m}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}
和
i
2
m
+
1
erfc
(
−
z
)
=
i
2
m
+
1
erfc
(
z
)
+
∑
q
=
0
m
z
2
q
+
1
2
2
(
m
−
q
)
−
1
(
2
q
+
1
)
!
(
m
−
q
)
!
.
{\displaystyle \mathrm {i} ^{2m+1}\operatorname {erfc} (-z)=\mathrm {i} ^{2m+1}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}\,.}
x
erf(x)
erfc(x)
x
erf(x)
erfc(x)
0.00
0.0000000
1.0000000
1.30
0.9340079
0.0659921
0.05
0.0563720
0.9436280
1.40
0.9522851
0.0477149
0.10
0.1124629
0.8875371
1.50
0.9661051
0.0338949
0.15
0.1679960
0.8320040
1.60
0.9763484
0.0236516
0.20
0.2227026
0.7772974
1.70
0.9837905
0.0162095
0.25
0.2763264
0.7236736
1.80
0.9890905
0.0109095
0.30
0.3286268
0.6713732
1.90
0.9927904
0.0072096
0.35
0.3793821
0.6206179
2.00
0.9953223
0.0046777
0.40
0.4283924
0.5716076
2.10
0.9970205
0.0029795
0.45
0.4754817
0.5245183
2.20
0.9981372
0.0018628
0.50
0.5204999
0.4795001
2.30
0.9988568
0.0011432
0.55
0.5633234
0.4366766
2.40
0.9993115
0.0006885
0.60
0.6038561
0.3961439
2.50
0.9995930
0.0004070
0.65
0.6420293
0.3579707
2.60
0.9997640
0.0002360
0.70
0.6778012
0.3221988
2.70
0.9998657
0.0001343
0.75
0.7111556
0.2888444
2.80
0.9999250
0.0000750
0.80
0.7421010
0.2578990
2.90
0.9999589
0.0000411
0.85
0.7706681
0.2293319
3.00
0.9999779
0.0000221
0.90
0.7969082
0.2030918
3.10
0.9999884
0.0000116
0.95
0.8208908
0.1791092
3.20
0.9999940
0.0000060
1.00
0.8427008
0.1572992
3.30
0.9999969
0.0000031
1.10
0.8802051
0.1197949
3.40
0.9999985
0.0000015
1.20
0.9103140
0.0896860
3.50
0.9999993
0.0000007
x
erfc(x)/2
1
7.86496e−2
2
2.33887e−3
3
1.10452e−5
4
7.70863e−9
5
7.6873e−13
6
1.07599e−17
7
2.09191e−23
8
5.61215e−30
9
2.06852e−37
10
1.04424e−45
11
7.20433e−55
12
6.78131e−65
13
8.69779e−76
14
1.51861e−87
15
3.6065e−100
16
1.16424e−113
17
5.10614e−128
18
3.04118e−143
19
2.45886e−159
20
2.69793e−176
21
4.01623e−194
22
8.10953e−213
23
2.22063e−232
24
8.24491e−253
25
4.15009e−274
26
2.8316e−296
27
2.61855e−319
^ Andrews, Larry C.; Special functions of mathematics for engineers 页面存档备份 ,存于互联网档案馆 )
^ 2.0 2.1 Greene, William H.; Econometric Analysis (fifth edition), Prentice-Hall, 1993, p. 926, fn. 11
^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. Handbook of Continued Fractions for Special Functions. Springer-Verlag . 2008. ISBN 978-1-4020-6948-2 ^ Winitzki, Sergei. A handy approximation for the error function and its inverse (PDF) . 6 February 2008 [2011-10-03 ] . [永久失效連結 ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 978-0-521-43064-7 ), 1992, page 214, Cambridge University Press.