同界角
在幾何學中,同界角(英語:Coterminal angles)是指兩個有向角(有標示起始邊與終邊的角)有著各自的角度量值(其量值可能相等),且共用同一對起始邊與終邊,即共享相同始邊和終邊的角度,但擁有不同的旋轉量,就稱為同界角[1]。同界角擁有相同的三角函數值,因此三角函數具有周期性。每個角皆有無限多個同界角,其量值可以為負,但必須是一個實數。
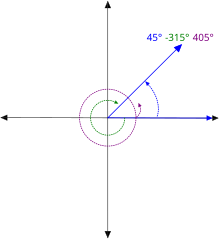
性質 编辑
每個同界角皆差360度,換句話說,每360度就會出現一個同界角[2]。每個同界角兩邊的向量內積與外積皆有相同的值。此外,任何角都可以找到最小正同界角和最大負同界角。
同界角可以如下定義:
同界角存在關係式:
亦可寫為:
或:
與三角函數關係 编辑
從三角函數的诱导公式可以得知同界角的存在,下表指出,任何三角函數,只要位移為 ,就會得到相同的函數值,因此 與 互為同界角。
| 移位 | 移位 和 的周期 |
移位 、 、 和 的周期 |
|---|---|---|
另外,從簡單的三角方程中,也可以找到同界角,例如:
- 考慮方程 有無限多組解,其中 為一個解且為最小正同界角,其餘解皆與 或是- 互為同界角。
最小正同界角與最大負同界角 编辑
同界角通常有無窮多個,因此在計算一些角度或三角函數抑或是一些週期函數的解時,會取最接近零的同界角。這類同界角又可以再分成最小正同界角與最大負同界角。其中,最小正同界角恆為正,通常解某些具週期性的方程的主值時,是使用最小正同界角。最小正同界角在0到 (360度)之間的最小正同界角與原始角相同,當原始角為 (360度)或 (360度)的倍數時,最小正同界角為零;最大負同界角恆為負,在 (負360度)到0之間的最大負同界角與原始角相同。
參見 编辑
參考文獻 编辑
- ^ Neal, Karla V.; R. David Gustafson, Jeffrey D. Hughes. Coterminal angles. Precalculus, 1st ed.. Cengage Learning. : 第412頁. ISBN 1133712673. (原始内容存档于2019-10-18).
- ^ Slavin, Steve; Ginny Crisonino. Circle. Wiley Self-Teaching Guides第 155 卷. John Wiley & Sons. 2004-10-28: 第90頁. ISBN 0471680192. (原始内容存档于2019-11-06).