十一面體

在幾何學中，十一面體（英語：Hendecahedron）是指具有十一個面的多面體。沒有任何十一面體是正十一面體，也就是說找不到面由正多邊形組成且每個面全等、每個角相等的十一面體。

十一面體

部分的十一面體
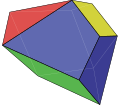雙對稱十一面體	五角錐台錐
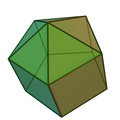正五角錐柱	截頂角五方偏方面體
側錐六角柱	二側錐三角柱

命名

十一面體的英文是Hendecahedron，其命名方式為Hen-代表一，deca代表十，然後結合多面體字尾-hedron，就得到十一面體Hendecahedron。

常見的十一面體

在所有凸十一面體中，包含鏡射像共有440,564種拓樸結構明顯差異的凸十一面體。拓樸結構有明顯差異意味著兩種多面體無法透過移動頂點位置、扭曲或伸縮來相互變換的多面體，例如五角錐柱和九角柱無論如何變形都無法互相變換，因此拓樸結構不同，但九角柱和九角錐台可以透過伸縮其中一個九邊形面來彼此互換，因此三角柱和三角錐台在拓樸上並無明顯差異。

常見的十一面體有錐體和柱體、部分的詹森多面體和半正多面體，此處的半正多面體並非阿基米德立體，而是正九角柱。

其他十一面體還有九角柱、十角錐、正五角錐反角柱的對偶、雙對稱十一面體等多面體，其中雙對稱十一面體可以密鋪空間。

三角罩帳

正三角罩帳

三角罩帳是指以三角形為底的罩帳，是一種十一面體，由1個三角形頂面、1個六邊形底面、3個五邊形側面和6個三角形側面組成，共有11個面、21條邊和12個頂點，其中頂面的三角形與底面的六邊形互相平行，側面的三角形與五邊形交錯地圍繞軸分佈在周圍。

以正三角形為底的三角罩帳稱為正三角罩帳，其僅有頂面和底面為正多邊形，分別為頂面的正三邊形和底面的正六邊形，側面可能可以存在正三角形或存在正五邊形，但有正三角形面時，五邊形最多僅能是等邊不等角的非正五邊形；有正五邊形面時，三角形會出現等腰三角形，故不屬於詹森多面體。唯一屬於詹森多面體的罩帳僅有正五角罩帳。

正三角罩帳的對稱群為C_3v群，階數為6階。

截半三角柱

截半三角柱的旋轉動畫

在幾何學中，截半三角柱是指經過截半變換後的三角柱，是一種十一面體，其側面是正方形、底面是正三角形，另外還有6個等腰三角形面。

截半三角柱可由三角柱將邊的中點當作新的頂點，舊的頂點消失，來構造，換句話說，即是用三角柱由一條棱斬到另一條棱的中點（即斬去三角柱的頂點，但不是截角）而成。

其具有D_3h二面體群的對稱性。

詹森多面體

在十一面體中，有3個是詹森多面體，它們分別為:正五角錐柱、二側錐三角柱、側錐六角柱。

名稱	種類	圖像	編號	頂點	邊	面	面的種類	對稱性	展開圖
正五角錐柱	角錐柱		J9	11	20	11	5個正三角形 5個正方形 1個正五邊形	C5v, [5], (*55)
二側錐三角柱	錐體與柱體的組合		J50	8	17	11	10個正三角形 1個正方形	C2v
側錐六角柱	錐體與柱體的組合		J54	8	17	11	4個正三角形 5個正方形 2個六邊形	C2v

九角柱

正九角柱

主條目：九角柱

九角柱是一種底面為九邊形的柱體，是十一面體的一種，由11個面、27條邊和18個頂點組成，對偶多面體為雙九角錐。正九角柱代表每個面都是正多邊形的九角柱，其每個頂點都是2個正方形和1個九邊形的公共頂點，因此具有每個角等角的性質，可以歸類為半正十一面體。而頂點都是2個正方形和1個九邊形的公共頂點的這種頂角，在頂點圖中以$4{.}4{.}9$表示。正九角柱在施萊夫利符號中可以利用{9}×{} 或 t{2, 9}來表示；在考克斯特—迪肯符號中可以利用來表示；在威佐夫符號中可以利用2 9 | 2來表示；在康威多面體表示法中可以利用P9來表示。若一個正九角柱底邊的邊長為$s$、高為$h$，則其體積$V$和表面積$S$為：

$V={\frac {9hs^{2}\cot {\frac {\pi }{9}}}{4}}\approx 6.18182hs^{2}$

$S=9s\left(h+{\frac {1}{2}}s\cot {\frac {\pi }{9}}\right)\approx 9s\left(h+1.37374s\right)$

十角錐

十角錐是一種底面為十邊形的錐體，是十一面體的一種，由11個面、20條邊和11個頂點組成，其對偶多面體是自己本身。正十角錐是一種底面為正十邊形的十角錐。若一個正十角錐底邊的邊長為$s$、高為$h$，則其體積$V$和表面積$S$為：

$V={\frac {5{\sqrt {5+2{\sqrt {5}}}}}{6}}hs^{2}\approx 2.56474hs^{2}$

$S={\frac {5s\left({\sqrt {4h^{2}+\left(5+2{\sqrt {5}}\right)s^{2}}}+{\sqrt {5+2{\sqrt {5}}}}s\right)}{2}}\approx 2.5s\left({\sqrt {4h^{2}+9.47214s^{2}}}+3.07768s\right)$

十一面體列表

名稱	種類	圖像	符號	頂點	邊	面	χ	面的種類	對稱性	展開圖
九角柱	稜柱體		t{2,9} {9}x{}	18	27	11	2	2個九邊形 9個矩形	D9h, [9,2], (*922), order 36
十角錐	稜錐體		( )∨{10}	11	20	11	2	1個十邊形 10個三角形	C10v, [10], (*10 10)
五角錐柱	角錐柱 詹森多面體		P5+Y5	11	20	11	2	5個三角形 5個正方形 1個五邊形	C5v, [5], (*55)
五角錐台錐	截角雙錐			11	20	11	2	1個五邊形 5個梯形 5個三角形	C5v, [5], (*55)
三角罩帳	罩帳			12	21	11	2	1個三角形頂面 1個六邊形底面 3個五邊形側面 6個三角形側面	C3v, [3], (*33), order 6
截頂角五方偏方面體	截頂角偏方面體			16	25	11	2	1個五邊形底面 5個五邊形側面 5個鷂形側面	C5v, [5], (*55)
截半三角柱				9	18	11	2	2個三角形 3個正方形 6個等腰三角形	D3h, [3,2], (*322), order 12
截半雙三角錐				9	18	11	2	3個正方形 8個三角形	D3h, [3,2], (*223) order 12
雙對稱十一面體	空間充填多面體			11	20	11	2	4個箏形 2個菱形 4個等腰三角形 1個正方形

在化學中

在化學中，將十八面體硼烷離子([B₁₁H₁₁]²⁻)的氫全部去掉後，可以得到一個結構，它是十八面體，再將每個硼原子做垂直於重心到硼原子的面，可構造成新的多面體，即為十八面體硼烷結構的對偶多面體，也是十一面體之一。

雙對稱十一面體

雙對稱十一面體（Bisymmetric Hendecahedron）是十一面體的一種多面體

柏拉圖和阿基米德立體，只有少數可以密鋪於空間，也就是說堆砌在一起，不留空隙，以填補空間。Guy Inchbald描述了一個有趣的多面體，可以以令人驚訝的方式利用11面體完成空間的密鋪。

圖像	旋轉動畫	展開圖

曾有人提出一個十一面體，它的面數和頂點數是相同的，經過扭曲後，會得到不同的特性。最對稱的自身對偶十一面體是雙對稱十一面體，它之所以會稱為雙對稱是因為它有兩個對稱面。