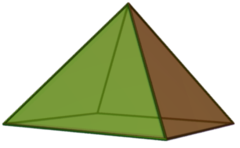
四角錐
 | ||
| 類別 | 詹森多面體 J92 – J1 – J2 | |
|---|---|---|
| 對偶多面體 | 正四角錐(自身對偶) | |
| 數學表示法 | ||
| 施萊夫利符號 | ()∨{4} | |
| 性質 | ||
| 面 | 5 | |
| 邊 | 8 | |
| 頂點 | 5 | |
| 歐拉特徵數 | F=5, E=8, V=5 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 正三角形×4 正方形×1 | |
| 頂點佈局 | 4(32.4) (34) | |
| 對稱性 | ||
| 對稱群 | C4v, [4], (*44) | |
| 旋轉對稱群 | C4, [4]+, (44) | |
| 特性 | ||
| 凸 | ||
| 圖像 | ||
| ||
種類
編輯長方錐
編輯底面為長方形的四角錐。
正四角錐
編輯底面為正方形的四角錐。通常是指側邊同時還是等腰三角形的四角錐。
特別地,側面也為正三角形的正四角錐是一種詹森多面體。
凹四角錐
編輯底面凹四邊形的四角錐。底面邊有交叉的也屬於凹四角錐(嚴格來說,應成為非凸四角錐)稱為交叉四角錐,其中星形帳塔可以分割成數個交叉四角錐。
詹森多面體
編輯在詹森多面體當中J1是一個以正方形為底並和其它四個正三角形所構成的四角錐,是詹森多面體中構造最簡單的一個,形似金字塔。同時它也是柏拉圖立體中正八面體的一半 。最早在1966年首先被諾曼·詹森命名和描述。
J1共有8個邊、5個面、5個頂點。若設其一邊為 ,體積為 ,高為 ,則:
相關多面體與鑲嵌
編輯| 正八面體可由兩個詹森多面體中的J1底面對底面疊在一起組成。 | 四角化六面體(Tetrakis Hexahedron)為卡塔蘭立體的其中一個,可由一個正方體的每一面疊一個正四角錐組成。 |
| 正二棱錐 | 正三棱錐 | 正四棱錐 | 正五棱錐 | 正六棱錐 | 正七棱錐 | 正八棱錐 | 正九棱錐 | 正十棱錐 | ... | 圓錐 |
|---|---|---|---|---|---|---|---|---|---|---|
| 球面鑲嵌 | 錐體 | 歐式鑲嵌 仿緊空間 |
雙曲鑲嵌 非緊空間 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 一角錐 C1v, [1] |
二角錐 C2v, [2] |
三角錐 C3v, [3] |
四角錐 C4v, [4] |
五角錐 C5v, [5] |
六角錐 C6v, [6] |
七角錐 C7v, [7] |
八角錐 C8v, [8] |
九角錐 C9v, [9] |
十角錐 C10v, [10] |
... |
無限角錐 C∞v, [∞] |
超無限角錐 Ciπ/λv, [iπ/λ] |
外部連結
編輯- Square Pyramid(頁面存檔備份,存於互聯網檔案館) Wolfram MathWorld
- Square Pyramid polyhedra.org
- Virtual Reality Polyhedra(頁面存檔備份,存於互聯網檔案館) www.georgehart.com: The Encyclopedia of Polyhedra (VRML model(頁面存檔備份,存於互聯網檔案館))
